
【题目】一平面上有32个点,其中无三点共线.证明:在这32个点中至少能找到2135个四点组,形成凸四边形的四个顶点.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的各棱长均为2,
的各棱长均为2, ![]() 面
面![]() ,E,F分别为棱
,E,F分别为棱![]() 的中点.
的中点.
(1)求证:直线BE∥平面![]() ;
;
(2)平面![]() 与直线AB交于点M,指出点M的位置,说明理由,并求三棱锥
与直线AB交于点M,指出点M的位置,说明理由,并求三棱锥![]() 的体积.
的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() (a>0,b>0)的左、右焦点分别为F1,F2,P为双曲线C上的一点,线段PF1与y轴的交点M恰好是线段PF1的中点,
(a>0,b>0)的左、右焦点分别为F1,F2,P为双曲线C上的一点,线段PF1与y轴的交点M恰好是线段PF1的中点,![]() ,其中O为坐标原点,则双曲线C的渐近线的斜率与离心率分别是( )
,其中O为坐标原点,则双曲线C的渐近线的斜率与离心率分别是( )
A. ±1,![]() B. 1,
B. 1,![]() C. ±2,
C. ±2,![]() D. 2,
D. 2,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年寒假,因为“新冠”疫情全体学生只能在家进行网上学习,为了研究学生网上学习的情况,某学校随机抽取![]() 名学生对线上教学进行调查,其中男生与女生的人数之比为
名学生对线上教学进行调查,其中男生与女生的人数之比为![]() ,抽取的学生中男生有
,抽取的学生中男生有![]() 人对线上教学满意,女生中有
人对线上教学满意,女生中有![]() 名表示对线上教学不满意.
名表示对线上教学不满意.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对线上教学是否满意 与性别有关”;
的把握认为“对线上教学是否满意 与性别有关”;
态度 性别 | 满意 | 不满意 | 合计 |
男生 | |||
女生 | |||
合计 | 100 |
(2)从被调查的对线上教学满意的学生中,利用分层抽样抽取![]() 名学生,再在这
名学生,再在这![]() 名学生中抽取
名学生中抽取![]() 名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
附: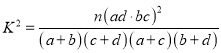 .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】低密度脂蛋白是一种运载胆固醇进入外周组织细胞的脂蛋白颗粒,可被氧化成氧化低密度脂蛋白,当低密度脂蛋白,尤其是氧化修饰的低密度脂蛋白过量时,它携带的胆固醇便积存在动脉壁上,久了容易引起动脉硬化,因此低密度脂蛋白被称为“坏的胆固醇”.为了调查某地中年人的低密度脂蛋白浓度是否与肥胖有关,随机调查该地100名中年人,得到2×2列联表如下:
肥胖 | 不肥胖 | 总计 | |
低密度脂蛋白不高于 | 12 | 63 | 75 |
低密度脂蛋白高于 | 8 | 17 | 25 |
总计 | 20 | 80 | 100 |
由此得出的正确结论是( )
A.有10%的把握认为“该地中年人的低密度脂蛋白浓度与肥胖有关”
B.有10%的把握认为“该地中年人的低密度脂蛋白浓度与肥胖无关”
C.有90%的把握认为“该地中年人的低密度脂蛋白浓度与肥胖有关”
D.有90%的把握认为“该地中年人的低密度脂蛋白浓度与肥胖无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知曲线C的参数方程为![]() 为参数
为参数![]() ,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系.
,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系.
(1)求曲线C的极坐标方程;
(2)设直线l的极坐标方程为![]() ,若直线l与曲线C交于M,N两点,且
,若直线l与曲线C交于M,N两点,且![]() ,求直线l的直角坐标方程.
,求直线l的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“黄梅时节家家雨”“梅雨如烟暝村树”“梅雨暂收斜照明”![]() 江南梅雨的点点滴滴都流润着浓洌的诗情
江南梅雨的点点滴滴都流润着浓洌的诗情![]() 每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南Q镇
每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南Q镇![]() 年梅雨季节的降雨量
年梅雨季节的降雨量![]() 单位:
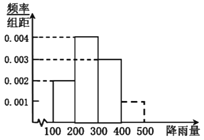
单位:![]() 的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
![]() Ⅰ
Ⅰ![]() “梅实初黄暮雨深”
“梅实初黄暮雨深”![]() 假设每年的梅雨天气相互独立,求Q镇未来三年里至少有两年梅雨季节的降雨量超过350mm的概率;
假设每年的梅雨天气相互独立,求Q镇未来三年里至少有两年梅雨季节的降雨量超过350mm的概率;
![]() Ⅱ
Ⅱ![]() “江南梅雨无限愁”
“江南梅雨无限愁”![]() 在Q镇承包了20亩土地种植杨梅的老李也在犯愁,他过去种植的甲品种杨梅,平均每年的总利润为28万元
在Q镇承包了20亩土地种植杨梅的老李也在犯愁,他过去种植的甲品种杨梅,平均每年的总利润为28万元![]() 而乙品种杨梅的亩产量
而乙品种杨梅的亩产量![]() 亩
亩![]() 与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为
与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为![]() 元
元![]() ,请你帮助老李排解忧愁,他来年应该种植哪个品种的杨梅可以使总利润
,请你帮助老李排解忧愁,他来年应该种植哪个品种的杨梅可以使总利润![]() 万元
万元![]() 的期望更大?
的期望更大?![]() 需说明理由
需说明理由![]()
降雨量 |
|
|
|
|
亩产量 | 500 | 700 | 600 | 400 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两名工人在同样条件下每天各生产100件产品,且每生产1件正品可获利20元,生产1件次品损失30元,甲、乙两名工人100天中出现次品件数的情况如表所示.
甲每天生产的次品数/件 | 0 | 1 | 2 | 3 | 4 |
对应的天数/天 | 40 | 20 | 20 | 10 | 10 |
乙每天生产的次品数/件 | 0 | 1 | 2 | 3 |
对应的天数/天 | 30 | 25 | 25 | 20 |
(1)将甲每天生产的次品数记为![]() (单位:件),日利润记为
(单位:件),日利润记为![]() (单位:元),写出
(单位:元),写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)按这100天统计的数据,分别求甲、乙两名工人的平均日利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com