【题目】已知平面α∥平面β，P是α，β外一点，过点P的直线m与α，β分别交于点A，C，过点P的直线n与α，β分别交于点B，D，且PA=6，AC=9，PD=8，则BD的长为（ ）
A.
B.
C.或24
D.或12
【答案】C
【解析】解：连接AB、CD；
①当点P在CA的延长线上，即P在平面α与平面β的同侧时，如图1；
∵α∥β，平面PCD∩α=AB，平面PCD∩β=CD，
∴AB∥CD，∴
=
；
∵PA=6，AC=9，PD=8，
∴
=
， 解得BD=
；
②当点P在线段CA上，即P在平面α与平面β之间时，如图2；
类似①的方法，可得=
，
∵PA=6，PC=AC﹣PA=9﹣6=3，PD=8，
∴
=
， 解得PB=16；
∴BD=PB+PD=24；
综上，BD的长为或24．
故选：C．
【考点精析】掌握平面与平面平行的性质是解答本题的根本，需要知道如果两个平面同时与第三个平面相交，那么它们的交线平；可以由平面与平面平行得出直线与直线平行．
科目：高中数学 来源： 题型：
【题目】写出下列命题的否定，并判断其真假：
(1)p：末位数字为9的整数能被3整除；
(2)p：有的素数是偶数；
(3)p：至少有一个实数x，使x2＋1＝0；
(4)p：x，y∈R，x2＋y2＋2x－4y＋5＝0.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆心为C的圆：（x﹣a）2+（y﹣b）2=8（a，b为正整数）过点A（0，1），且与直线y﹣3﹣2 
=0相切．
（1）求圆C的方程；
（2）若过点M（4，﹣1）的直线l与圆C相交于E，F两点，且 
=0．求直线l的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
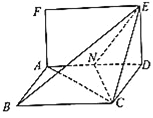
【题目】已知矩形
和菱形
所在平面互相垂直，如图，其中
， 
， 
，点
为线段
的中点．
（Ⅰ）试问在线段
上是否存在点
，使得直线
平面
？若存在，请证明
平面
，并求出
的值，若不存在，请说明理由；
（Ⅱ）求二面角
的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系中，O为坐标原点，A、B、C三点满足 
= 
+ 
．
（1）求证：A、B、C三点共线；
（2）求 
的值；
（3）已知A（1，cosx）、B（1+cosx，cosx），x∈[0， 
]，f（x）= 
﹣（2m+ ）| 
|的最小值为﹣ 
，求实数m的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在海岛
上有一座海拔
的山峰，山顶设有一个观察站
，有一艘轮船按一固定方向做匀速直线航行，上午
时，测得此船在岛北偏东
、俯角为
的
处，到
时，又测得该船在岛北偏西
、俯角
为的
处.
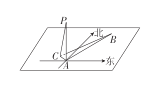
（1）求船的航行速度；
（2）求船从
到
行驶过程中与观察站
的最短距离.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》，某校计划开设八门研学旅行课程，并对全校学生的选课意向进行调查(调查要求全员参与，每个学生必须从八门课程中选出唯一一门课程).本次调查结果如下.
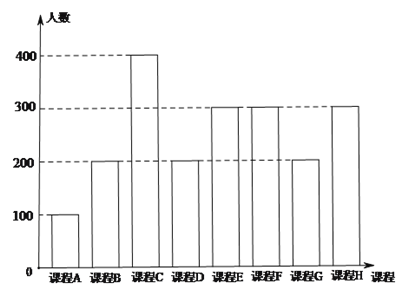
图中，课程
为人文类课程，课程
为自然科学类课程.为进一步研究学生选课意向，结合上面图表，采取分层抽样方法从全校抽取1%的学生作为研究样本组（以下简称“组
”）.
（Ⅰ）在“组
”中，选择人文类课程和自然科学类课程的人数各有多少？
（Ⅱ）某地举办自然科学营活动，学校要求：参加活动的学生只能是“组
”中选择
课
程或
课程的同学，并且这些同学以自愿报名缴费的方式参加活动. 选择
课程的学生中有
人参加科学营活动，每人需缴纳
元，选择
课程的学生中有
人参加该活动，每人需缴纳
元.记选择
课程和
课程的学生自愿报名人数的情况为
，参加活动的学生缴纳费用总和为
元.
①当
时，写出
的所有可能取值；
②若选择
课程的同学都参加科学营活动，求
元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
