
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,记函数
时,记函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ,求
,求![]() 的取值范围.
的取值范围.
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】“互联网![]() ”是“智慧城市”的重要内士,
”是“智慧城市”的重要内士,![]() 市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费
市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费![]() .为了解免费
.为了解免费![]() 在
在![]() 市的使用情况,调査机构借助网络进行了问卷调查,并从参与调査的网友中抽取了
市的使用情况,调査机构借助网络进行了问卷调查,并从参与调査的网友中抽取了![]() 人进行抽样分析,得到如下列联表(单位:人):
人进行抽样分析,得到如下列联表(单位:人):
经常使用免费WiFi | 偶尔或不用免费WiFi | 合计 | |
45岁及以下 | 70 | 30 | 100 |
45岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,判断是否有![]() 的把握认为
的把握认为![]() 市使用免费
市使用免费![]() 的情况与年龄有关;
的情况与年龄有关;
(2)将频率视为概率,现从该市![]() 岁以上的市民中用随机抽样的方法每次抽取
岁以上的市民中用随机抽样的方法每次抽取![]() 人,共抽取
人,共抽取![]() 次.记被抽取的
次.记被抽取的![]() 人中“偶尔或不用免费
人中“偶尔或不用免费![]() ”的人数为
”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列,数学期望
的分布列,数学期望![]() 和方差
和方差![]() .
.
附: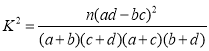 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线![]() 经过点
经过点![]() ,倾斜角
,倾斜角![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() .
.
(Ⅰ)求曲线C的直角坐标方程并写出直线l的参数方程;
(Ⅱ)直线l与曲线C的交点为A,B,求点P到A、B两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“珠算之父”程大位是我国明代著名的数学家,他的应用巨著《算法统综》中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节四升五,上梢四节三升八,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明.”((注)四升五:4.5升,次第盛:盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节竹的容积为
A. 2.2升B. 2.3升
C. 2.4升D. 2.5升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知在四棱锥![]() 中,底面
中,底面![]() 是边长为4的正方形,
是边长为4的正方形,![]() 是正三角形,平面
是正三角形,平面![]() 平面
平面![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 是线段
是线段![]() 上一点,求三棱锥
上一点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)利用“五点法”画出函数![]() 在长度为一个周期的闭区间的简图.
在长度为一个周期的闭区间的简图.
列表:
| |||||
x | |||||
y |
作图:
(2)并说明该函数图象可由![]() 的图象经过怎么变换得到的.
的图象经过怎么变换得到的.
(3)求函数![]() 图象的对称轴方程.
图象的对称轴方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com