解:(1)对于a=2,x∈[2,3],f(x)=e
|x-3|+e
|x-2|+1=e
3-x+e
x-1(3分)
≥2
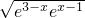
=2e,
当且仅当e
3-x=e
x-1,即x=2时等号成立,∴f(x)
min=2e.(6分)
(2)|f
1(x)-f
2(x)|=f
2(x)-f
1(x)对于任意的实数x恒成立,
即f
1(x)≤f
2(x)对于任意的实数x恒成立,亦即e
|x-2a+1|≤e
|x-a|+1对于任意的实数x恒成立,
∴|x-2a+1|≤|x-a|+1,即|x-2a+1|-|x-a|≤1对于任意的实数x恒成立.(9分)
又|x-2a+1|-|x-a|≤|(x-2a+1)-(x-a)|=|-a+1|对于任意的实数x恒成立,故只需
|-a+1|≤1,解得0≤a≤2,∴a的取值范围为0≤a≤2.(12分)
(3)g(x)=
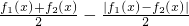
=
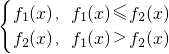
(13分)
∵f
1(x)与f
2(x)的底数都同为e,外函数都单调递增
∴比较f
1(x)与f
2(x)的大小关系,只须比较|x-2a+1|与|x-a|+1的大小关系
令F
1(x)=|x-2a+1|,F
2(x)=|x-a|+1,
G(x)=
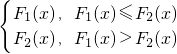
其中4≤a≤6,x∈[1,6](14分)
∵4≤a≤6∴2a-1≥a≥1,令2a-1-x=1,得x=2a-2,由题意可以如下图象:
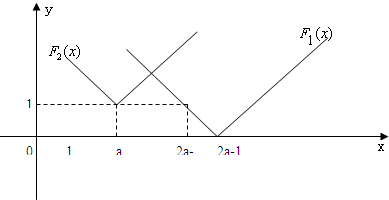
(15分)
当4≤a≤6时,a≤6≤2a-2,G(x)
min=F
2(a)=1,g(x)
min=e
1=e;(18分)
分析:(1)对于a=2,x∈[2,3],去掉绝对值得f(x)=e
3-x+e
x-1(3分),利用基本不等式积为定值,和有最小值即可求出函数的最小值,注意等号成立的条件;
(2)根据条件可知f
1(x)≤f
2(x)对于任意的实数x恒成立,转化成|x-2a+1|-|x-a|≤1对于任意的实数x恒成立,然后利用绝对值不等式进行求解即可求出参数a的范围;
(3)f
1(x)与f
2(x)的底数都同为e,外函数都单调递增,比较f
1(x)与f
2(x)的大小关系,只须比较|x-2a+1|与|x-a|+1的大小关系,则令F
1(x)=|x-2a+1|,F
2(x)=|x-a|+1,则G(x)=
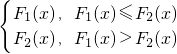
其中4≤a≤6,x∈[1,6],结合图形可知当4≤a≤6时G(x)
min=F
2(a)=1,g(x)
min=e
1=e.
点评:本题主要考查了基本不等式在最值问题中的应用,以及函数的最值及其几何意义和恒成立问题等有关知识,解决本题的关键是等价转化,以及数形结合,分类讨论的思想,难点是绝对值如何去.

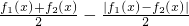 在x∈[1,6]上的最小值.
在x∈[1,6]上的最小值.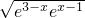 =2e,
=2e,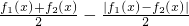 =
=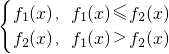 (13分)
(13分)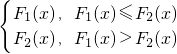 其中4≤a≤6,x∈[1,6](14分)
其中4≤a≤6,x∈[1,6](14分) (15分)
(15分)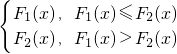 其中4≤a≤6,x∈[1,6],结合图形可知当4≤a≤6时G(x)min=F2(a)=1,g(x)min=e1=e.
其中4≤a≤6,x∈[1,6],结合图形可知当4≤a≤6时G(x)min=F2(a)=1,g(x)min=e1=e.
