
【题目】已知函数 ![]() .
.
(1)求函数f(x)的定义域;
(2)若函数f(x)在区间[10,+∞)上是增函数,求实数a的取值范围.
【答案】
(1)解:若函数 ![]() 的真数为正,
的真数为正,
则(ax﹣1)(x﹣1)>0,
当a=1时,函数f(x)的定义域为{x|x≠1};
当0<a<1时,函数f(x)的定义域为 ![]() ;
;
当a>1时 ![]()
(2)解: ![]() ,
,
函数f(x)在区间[10,+∞)上是增函数,
只需要 ![]() 在区间[10,+∞)上是增函数,且大于零.
在区间[10,+∞)上是增函数,且大于零.
即当x1>x2≥10时, ![]() 恒成立.
恒成立.
∵x2﹣x1<0,(x1﹣1)(x2﹣1)>0,
∴k﹣1<0即可.
![]() 在区间[10,+∞)上是增函数,
在区间[10,+∞)上是增函数,
要使g(x)>0恒成立,
只要 ![]() ,
,
∴ ![]()
【解析】(1)若函数 ![]() 的真数为正,则(ax﹣1)(x﹣1)>0,分类讨论,可得不同情况下函数f(x)的定义域;(2)若函数f(x)在区间[10,+∞)上是增函数,只需要
的真数为正,则(ax﹣1)(x﹣1)>0,分类讨论,可得不同情况下函数f(x)的定义域;(2)若函数f(x)在区间[10,+∞)上是增函数,只需要 ![]() 在区间[10,+∞)上是增函数,且大于零恒成立,进而得到实数a的取值范围.
在区间[10,+∞)上是增函数,且大于零恒成立,进而得到实数a的取值范围.
【考点精析】根据题目的已知条件,利用函数的定义域及其求法和函数单调性的判断方法的相关知识可以得到问题的答案,需要掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.


科目:高中数学 来源: 题型:
【题目】将函数f(x)=cos(x+φ)的图象上每点的横坐标缩短为原来的 ![]() 倍(纵坐标不变),再将所得的图象向左平移
倍(纵坐标不变),再将所得的图象向左平移 ![]() 个单位长度后得到的图象关于坐标原点对称,则下列直线中是函数f(x)图象的对称轴的是( )
个单位长度后得到的图象关于坐标原点对称,则下列直线中是函数f(x)图象的对称轴的是( )
A.x=﹣ ![]()
B.x= ![]()
C.x=﹣ ![]()
D.x= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(2ax+1)+ ![]() ﹣x2﹣2ax(a∈R).
﹣x2﹣2ax(a∈R).
(1)若x=2为f(x)的极值点,求实数a的值;
(2)若y=f(x)在[3,+∞)上为增函数,求实数a的取值范围;
(3)当a=﹣ ![]() 时,方程f(1﹣x)=
时,方程f(1﹣x)= ![]() 有实根,求实数b的最大值.
有实根,求实数b的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() :
:![]() (
(![]() )的四个顶点,四边形
)的四个顶点,四边形![]() 是圆
是圆![]() :
:![]() 的外切平行四边形,其面积为
的外切平行四边形,其面积为![]() .椭圆
.椭圆![]() 的内接
的内接![]() 的重心(三条中线的交点)为坐标原点
的重心(三条中线的交点)为坐标原点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)![]() 的面积是否为定值?若是,求出该定值,若不是,请说明理由.
的面积是否为定值?若是,求出该定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】专家研究表明,![]() 2.5是霾的主要成份,在研究
2.5是霾的主要成份,在研究![]() 2.5形成原因时,某研究人员研究了
2.5形成原因时,某研究人员研究了![]() 2.5与燃烧排放的
2.5与燃烧排放的![]() 、
、![]() 、
、![]() 、
、![]() 等物质的相关关系.下图是某地某月
等物质的相关关系.下图是某地某月![]() 2.5与
2.5与![]() 和
和![]() 相关性的散点图.
相关性的散点图.
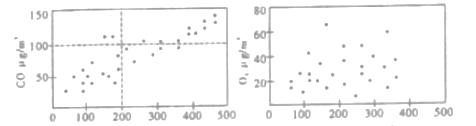
(Ⅰ)根据上面散点图,请你就![]() ,
,![]() 对
对![]() 2.5的影响关系做出初步评价;
2.5的影响关系做出初步评价;
(Ⅱ)根据有关规定,当![]() 排放量低于
排放量低于![]() 时
时![]() 排放量达标,反之为
排放量达标,反之为![]() 排放量超标;当
排放量超标;当![]() 2.5值大于
2.5值大于![]() 时雾霾严重,反之雾霾不严重.根据
时雾霾严重,反之雾霾不严重.根据![]() 2.5与
2.5与![]() 相关性的散点图填写好下面
相关性的散点图填写好下面![]() 列联表,并判断有多大的把握认为“雾霾是否严重与排放量有关”:
列联表,并判断有多大的把握认为“雾霾是否严重与排放量有关”:
雾霾不严重 | 雾霾严重 | 总计 | |
| |||
| |||
总计 |
(Ⅲ)我们知道雾霾对交通影响较大.某市交通部门发现,在一个月内,当![]() 排放量分别是60,120,180时,某路口的交通流量(单位:万辆)一次是800,600,200,而在一个月内,
排放量分别是60,120,180时,某路口的交通流量(单位:万辆)一次是800,600,200,而在一个月内,![]() 排放量是60,120,180的概率一次是
排放量是60,120,180的概率一次是![]() ,
,![]() ,
,![]() (
(![]() ),求该路口一个月的交通流量期望值的取值范围.
),求该路口一个月的交通流量期望值的取值范围.
附:
0.100 | 0.050 | 0.010 | 0.001 | |
2.706 | 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若偶函数f(x)在(﹣∞,﹣1]上是增函数,则下列关系式中成立的是( )
A.f(﹣ ![]() )<f(﹣1)<f(2)
)<f(﹣1)<f(2)
B.f(﹣1)<f(﹣ ![]() )<f(2)??
)<f(2)??
C.f(2)<f(﹣1)<f(﹣ ![]() )
)
D.f(2)<f(﹣ ![]() )<f(﹣1)
)<f(﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com