
分析 (I)①利用Ω对于即可判断出函数f(x)=x不是Ω函数.②对于g(x)=sinπx是Ω函数,令T=-1,对任意x∈R,有Tf(x+T)=f(x)成立.
(II)(i)函数f(x)是Ω函数,可得存在非零常数T,Tf(x+T)=f(x),Tf(-x+T)=f(-x).又f(x)是偶函数,可得Tf(-x+T)=Tf(x+T),T≠0,化为:f(x+T)=f(-x+T),通过换元进而得出:f(2T+t)=f(t),因此函数f(x)是周期为2T的周期函数.
(ii)同(i)可以证明.
(III)当a>1时,假设函数f(x)=ax是Ω函数,则存在非零常数T,Tf(x+T)=f(x),可得Tax+T=ax,化为:TaT=1,即aT=$\frac{1}{T}$,此方程有非0 的实数根,即可证明.
解答 解:(I)①对于函数f(x)=x是Ω函数,假设存在非零常数T,Tf(x+T)=f(x),则T(x+T)=x,取x=0时,则T=0,与T≠0矛盾,因此假设不成立,即函数f(x)=x不是Ω函数.
②对于g(x)=sinπx是Ω函数,令T=-1,则sin(πx-π)=-sin(π-πx)=-sinπx.即-sin(π(x-1))=sinπx.
∴Tsin(πx+πT)=sinπx成立,即函数f(x)=sinπx对任意x∈R,有Tf(x+T)=f(x)成立.
(II)(i)证明:∵函数f(x)是Ω函数,∴存在非零常数T,Tf(x+T)=f(x),Tf(-x+T)=f(-x).
又f(x)是偶函数,∴f(-x)=f(x),∴Tf(-x+T)=Tf(x+T),T≠0,化为:f(x+T)=f(-x+T),
令x-T=t,则x=T+t,∴f(2T+t)=f(-t)=f(t),可得:f(2T+t)=f(t),因此函数f(x)是周期为2T的周期函数.
(ii)证明:∵函数f(x)是Ω函数,∴存在非零常数T,Tf(x+T)=f(x),Tf(-x+T)=f(-x).
又f(x)是奇函数,∴f(-x)=-f(x),∴-Tf(x+T)=Tf(-x+T),T≠0,化为:-f(x+T)=f(-x+T),
令x-T=t,则x=T+t,∴-f(2T+t)=f(-t)=-f(t),可得:f(2T+t)=f(t),因此函数f(x)是周期为2T的周期函数.
(III)证明:当a>1时,假设函数f(x)=ax是Ω函数,则存在非零常数T,Tf(x+T)=f(x),
∴Tax+T=ax,化为:TaTax=ax,∵ax>0,∴TaT=1,即aT=$\frac{1}{T}$,此方程有非0 的实数根,因此T≠0且存在,
∴当a>1时,函数f(x)=ax一定是Ω函数.
点评 本题考查了新定义、函数的奇偶性周期性、方程思想方法、换元方法,考查了推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | R | B. | {x|x≤-7或x≥3} | C. | {x|x≤-7或x>1} | D. | {x|-7≤x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
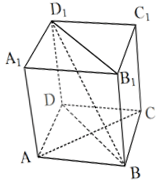 如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是正方形,且AB=1,D1D=$\sqrt{2}$
如图,在四棱柱ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是正方形,且AB=1,D1D=$\sqrt{2}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{5}{3}$ | C. | 4 | D. | -10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{5}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{5}+\frac{y^2}{2}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{10}+\frac{y^2}{16}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{3}{2}$) | B. | (0,$\frac{3}{2}$) | C. | (0,1)∪(1,$\frac{3}{2}$) | D. | (0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com