
【题目】如图,A、B两地相距100公里,两地政府为提升城市的抗疫能力,决定在A、B之间选址P点建造储备仓库,共享民生物资,当点P在线段AB的中点C时,建造费用为2000万元,若点P在线段AC上(不含点A),则建造费用与P、A之间的距离成反比,若点P在线段CB上(不含点B),则建造费用与P、B之间的距离成反比,现假设P、A之间的距离为x千米![]() ,A地所需该物资每年的运输费用为
,A地所需该物资每年的运输费用为![]() 万元,B地所需该物资每年的运输费用为
万元,B地所需该物资每年的运输费用为![]() 万元,
万元,![]() 表示建造仓库费用,
表示建造仓库费用,![]() 表示两地物资每年的运输总费用(单位:万元).
表示两地物资每年的运输总费用(单位:万元).
![]()
(1)求函数![]() 的解析式;
的解析式;
(2)若规划仓库使用的年限为![]() ,
,![]() ,求
,求![]() 的最小值,并解释其实际意义.
的最小值,并解释其实际意义.
【答案】(1)当![]() ,
,![]() ;当
;当![]() ,
,![]() ;(2)
;(2)![]() ,见解析
,见解析
【解析】
(1)由题意,设f(x)=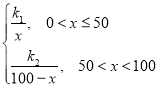 ,由f(50)=2000,求得k1与k2的值,则函数解析式可求;
,由f(50)=2000,求得k1与k2的值,则函数解析式可求;
(2)求出g(x)=2.5x+0.5(100﹣x)=2x+50,然后分段写出H(x),求导后再对n分类求解H(x)的最小值,并解释其实际意义.
解:(1)由题意,设f(x)=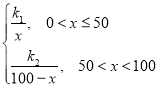 ,
,
由f(50)=2000,求得k1=k2=100000.
∴f(x)=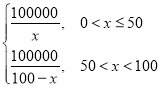 ;
;
(2)g(x)=2.5x+0.5(100﹣x)=2x+50,
若0<x≤50,则H(x)=f(x)+ng(x)=![]() ,
,
H′(x)=![]() ,由H′(x)=0,得x=100
,由H′(x)=0,得x=100![]() ,
,
若n∈N*且n≤20,则H(x)在(0,50]上单调递减,H(x)min=H(50)=2000+150n;
若n∈N*且n>20,则H(x)在(0,100![]() )上单调递减,在(100
)上单调递减,在(100![]() ,50)单调递增,
,50)单调递增,
∴![]() ;
;
若50<x<100,则H(x)=f(x)+ng(x)=![]() ,
,
H′(x)=![]() >0,H(x)在(50,100)上单调递增,
>0,H(x)在(50,100)上单调递增,
若n∈N*且n≤20,则H(x)>2000+150n;
若n∈N*且n>20,则H(x)>50n+![]() .
.
综上,若n∈N*且n≤20,则H(x)min=2000+150n;
若n∈N*且n>20,则![]() .
.
实际意义:建造储备仓库并使用n年,花费在建造仓库和两地物资运输总费用的最小值.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】如图所示,直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点P,使得直线
上是否存在点P,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2019年连续六个月的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示:

(1)由折线图可以看出,可用线性回归模型拟合月利润![]() (单位:百万元)与月份代码
(单位:百万元)与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测该公司2020年4月份的利润;
的线性回归方程,并预测该公司2020年4月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有A,B两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,但新材料的不稳定性会导致材料的使用寿命不同,现对A,B两种型号的新型材料对应的产品各100件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:

经甲公司测算平均每件新型材料每月可以带来6万元收人入,不考虑除采购成本之外的其他成本,A型号材料每件的采购成本为10万元,B型号材料每件的采购成本为12万元.假设每件新型材料的使用寿命都是整月数,且以频率作为每件新型材料使用寿命的概率,如果你是甲公司的负责人,以每件新型材料产生利润的平均值为决策依据,你会选择采购哪款新型材料?
参考数据:![]() ,
,![]() .
.
参考公式:回归直线方程![]() ,其中
,其中 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() ,直线
,直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的参数方程和圆
的参数方程和圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角的
的倾斜角的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国家批复成立江北新区后,南京市政府规划在新区内的一条形地块上新建一个全民健身中心,规划区域为四边形ABCD,如图![]() ,
,![]() ,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知
,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知![]() .
.
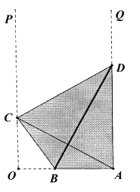
(1)若![]() ,求BD的长;
,求BD的长;
(2)问点C在何处时,规划区域的面积最小?最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院对治疗支气管肺炎的两种方案![]() ,
,![]() 进行比较研究,将志愿者分为两组,分别采用方案
进行比较研究,将志愿者分为两组,分别采用方案![]() 和方案
和方案![]() 进行治疗,统计结果如下:
进行治疗,统计结果如下:
有效 | 无效 | 合计 | |
使用方案 | 96 | 120 | |
使用方案 | 72 | ||
合计 | 32 |
(1)完成上述列联表,并比较两种治疗方案有效的频率;
(2)能否在犯错误的概率不超过0.05的前提下认为治疗是否有效与方案选择有关?
附: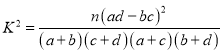 ,其中
,其中![]() .
.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 上一点
上一点![]() 作直线交抛物线E于另一点N.
作直线交抛物线E于另一点N.
(1)若直线MN的斜率为1,求线段![]() 的长.
的长.
(2)不过点M的动直线l交抛物线E于A,B两点,且以AB为直径的圆经过点M,问动直线l是否恒过定点.如果有求定点坐标,如果没有请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com