
【题目】设函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)如果对所有的![]() ,都有
,都有![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.(2)
上单调递增.(2)![]()
【解析】试题分析:
(1)求出导函数![]() ,解不等式
,解不等式![]() 得增区间,解不等式
得增区间,解不等式![]() 得减区间;
得减区间;
(2)不等式![]() 恒成立,可以变形为
恒成立,可以变形为![]() 恒成立,因此只要求出
恒成立,因此只要求出![]() 的最大值,由最大值小于或等于0可得,也要可变形为
的最大值,由最大值小于或等于0可得,也要可变形为![]() ,只要求得
,只要求得![]() 的最大值即可,这些最值可通过导数知识进行求解.
的最大值即可,这些最值可通过导数知识进行求解.
试题解析:
(1)![]() 的定义域为
的定义域为![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)法一:设![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() .
.
(i)当![]() 时,
时, ![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 上单调递减,而
上单调递减,而![]() ,
,
所以对所有的![]() ,
, ![]() ,即
,即![]() ;
;
(ii)当![]() 时,
时, ![]() ,若
,若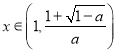 ,则
,则![]() ,
, ![]() 单调递增,
单调递增,
而![]() ,所以当
,所以当 时,
时, ![]() ,即
,即![]() ;
;
(iii)当![]() 时,
时, ![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 单调递增,而
单调递增,而![]() ,
,
所以对所有的![]() ,
, ![]() ,即
,即![]() ;
;
综上, ![]() 的取值范围是
的取值范围是![]() .
.
法二:当![]() 时,
时, ![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,当
,当![]() 时,
时, ![]() ,
,
于是![]() 在
在![]() 上为减函数,从而
上为减函数,从而![]() ,因此
,因此![]() ,
,
于是![]() 在
在![]() 上为减函数,所以当
上为减函数,所以当![]() 时
时![]() 有最大值
有最大值![]() ,
,
故![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】(文)已知矩形ABB1A1是圆柱体的轴截面,O、O1分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为2:1,且该圆柱体的体积为32π,如图所示. 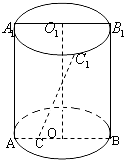
(1)求圆柱体的侧面积S侧的值;
(2)若C1是半圆弧 ![]() 的中点,点C在半径OA上,且OC=
的中点,点C在半径OA上,且OC= ![]() OA,异面直线CC1与BB1所成的角为θ,求sinθ的值.
OA,异面直线CC1与BB1所成的角为θ,求sinθ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:已知四棱锥P﹣ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证: 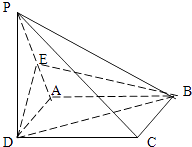
(1)PC∥平面EBD.
(2)平面PBC⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关注的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在[25,30),[55,60)的被调查者中赞成“延迟退休”的人数分别是3人和2人.现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(I)求年龄在[25,30)的被调查者中选取的2人都赞成“延迟退休”的概率;
(II)若选中的4人中,不赞成“延迟退休”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x3+2x2﹣4x+5在[﹣4,1]上的最大值和最小值分别是( )
A.13, ![]()
B.4,﹣11
C.13,﹣11
D.13,最小值不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 和直线
和直线![]() ,直线
,直线![]() ,
, ![]() 都经过圆
都经过圆![]() 外定点
外定点![]() .
.
(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,与
两点,与![]() 交于
交于![]() 点,且线段
点,且线段![]() 的中点为
的中点为![]() ,
,
求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题共14分)
如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 是菱形,
是菱形, ![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]()
(Ⅱ)若![]() 求
求![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(Ⅲ)当平面![]() 与平面
与平面![]() 垂直时,求
垂直时,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体![]() 中,
中,![]() ,
,![]() 是棱
是棱![]() 上的一点.
上的一点.
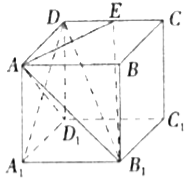
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)若![]() 是棱
是棱![]() 的中点,在棱
的中点,在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出线段
?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com