已知二次函数f(x)满足f(x+1)+f(x-1)=2x2-4x.
(1)求函数f(x)的解析式;
(2)若f(x)>a在x∈[-1,2]上恒成立,求实数a的取值范围;
(3)求当x∈[0,a](a>0)时f(x)的最大值g(a).
解:(1)设二次函数f(x)=ax
2+bx+c(a≠0)
∵f(x+1)+f(x-1)=2x
2-4x
∴a(x+1)
2+b(x+1)+c+a(x-1)
2+b(x-1)+c=2x
2-4x
∴2ax
2+2bx+2a+2c=2x
2-4x
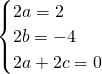
∴f(x)=x
2-2x-1( 5分)
(2)∵f(x)=x
2-2x-1=(x-1)
2-2在x∈[-1,2]上的最小值为f(1)=-2( 8分)
∵f(x)>a在x∈[-1,2]上恒成立
∴a<-2( 10 分 )
(3))∵f(x)=x
2-2x-1=(x-1)
2-2的对称轴x=1
①当0<a≤2时,根据二次函数的性质可得,f(x)
max=f(2)=-1
②a>2时,根据二次函数的性质可得,f(x)
max=f(a)=a
2-2a-1
综上可得,g(a)=
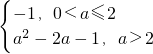
(16分)
分析:(1)可设二次函数f(x)=ax
2+bx+c(a≠0)然后求出f(x+1),f(x-1)再代入条件f(x+1)+f(x-1)=2x
2-4x中可得方程两边对应系数相等即可求出a,b,c的值从而求出二次函数f(x)的解析式.
(2)由f(x)>a在x∈[-1,2]上恒成立,则只要a<f(x)
min,可求
(3))f(x)=x
2-2x-1=(x-1)
2-2的对称轴x=1,需要讨论区间端点0,a与对称轴远近,①当0<a≤2时,f(x)
max=f(2)=-1②a>2时,f(x)
max=f(a)=a
2-2a-1
点评:本题主要考察利用待定系数法求解二次函数解析式.解题的关键是会设二次函数f(x)=ax
2+bx+c(a≠0)的解析式,二次函数在闭区间上的最值的求解.

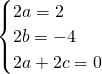
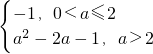 (16分)
(16分)
