
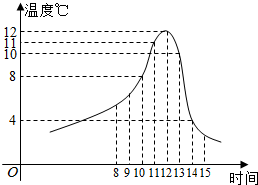
 某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系t=$\left\{\begin{array}{l}{64,x≤0}\\{{2}^{kx+6},x>0}\end{array}\right.$且该食品在4℃的保鲜时间是16小时.已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示,给出以下四个结论:
某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系t=$\left\{\begin{array}{l}{64,x≤0}\\{{2}^{kx+6},x>0}\end{array}\right.$且该食品在4℃的保鲜时间是16小时.已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示,给出以下四个结论:分析 根据食品在4℃的保鲜时间是16小时.求出k值,进而逐一分析四个结论的真假,可得答案.
解答 解:∵食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系t=$\left\{\begin{array}{l}{64,x≤0}\\{{2}^{kx+6},x>0}\end{array}\right.$且该食品在4℃的保鲜时间是16小时.已
∴24k+6=16,即4k+6=4,解得:k=$-\frac{1}{2}$,
∴t=$\left\{\begin{array}{l}64,x≤0\\{2}^{-\frac{1}{2}x+6},x>0\end{array}\right.$,
当x=6时,t=8,故①该食品在6℃的保鲜时间是8小时,正确;
②当x∈[-6,0]时,保鲜时间恒为64小时,当x∈(0,6]时,该食品的保鲜时间t随看x增大而逐渐减少,故错误;
③到了此日10时,温度超过8度,此时保鲜时间不超过4小时,故到13时,甲所购买的食品不在保鲜时间内,故错误;
④到了此日14时,甲所购买的食品已然过了保鲜时间,故正确,
故正确的结论的序号为:①④,
故答案为:①④.
点评 本题以命题的真假判断为载体,考查了函数在实际生活中的应用,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -9 | B. | -7 | C. | 1 | D. | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com