
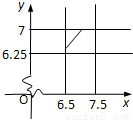
 (6分)
(6分)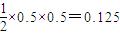
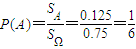 .(11分)
.(11分) .(12分)
.(12分) 求解.
求解. 

 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
假设某人定了鲜奶,送奶工可能在早上6:30~7:30之间把鲜奶送到他家,他离开家去上学的时间是6:15~7:00之间,设送奶工到达他家的时间是![]() ,他离开家的时间是
,他离开家的时间是![]() .用数对
.用数对![]() 表示可能的试验结果,则全部事件组成的集合
表示可能的试验结果,则全部事件组成的集合![]() .
.
(1)用集合表示他能在离家前喝到鲜奶的事件A;
(2)他能在离家前喝到鲜奶的概率是多少?
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省揭阳市揭东县云路中学高三(上)12月月考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com