
 如图,在四边形ABCD中,AB=4,BC=3,CD=2,DA=1,四边形的四个角分别记为A,B,C,D.
如图,在四边形ABCD中,AB=4,BC=3,CD=2,DA=1,四边形的四个角分别记为A,B,C,D.分析 (1))△ABD中,BD2=16+1-2×4×1×cosA,①,△BCD中,BD2=9+4-2×3×2×cosC,②,A+C=π,①+②,可求BD的长度.
(2)先计算S,T,由(1)可得2cosA-3cosC=1,利用配方法求S2+T2的最大值.
解答 解:(1)△ABD中,BD2=16+1-2×4×1×cosA,①
△BCD中,BD2=9+4-2×3×2×cosC,②
∵A+C=π,
∴①+②,可得2BD2=30,∴BD=$\sqrt{15}$;
(2)由(1)可得2cosA-3cosC=1,
S=$\frac{1}{2}•4•1•sinA$=2sinA,T=$\frac{1}{2}•3•2•sinC$=3sinC,
∴S2+T2=4sin2A+9sin2C=4-(3cosC+1)2+9sin2C=-18cos2C-6cosC+12=-18(cosC+$\frac{1}{6}$)2+12.5,
∴cosC=-$\frac{1}{6}$,S2+T2的最大值为12.5.
点评 本题考查余弦定理的运用,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面为正方形,PA⊥底面ABCD,E、F分别为AB、PD的中点.
如图,四棱锥P-ABCD的底面为正方形,PA⊥底面ABCD,E、F分别为AB、PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
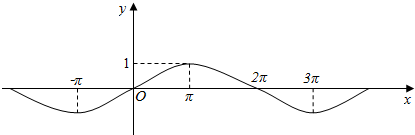
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平面就是平行四边形 | |
| B. | 空间任意三点可以确定一个平面 | |
| C. | 两两相交的三条直线可以确定一个平面 | |
| D. | 空间四点不共面,则其中任意三点不共线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{20}{31}$ | C. | $\frac{9}{14}$ | D. | $\frac{11}{17}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com