
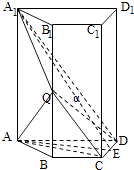
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1、C、D三点的平面记为α,BB1与α的交点为Q. 
(1)证明:Q为BB1的中点;
(2)求此四棱柱被平面α所分成上下两部分的体积之比;
(3)若AA1=4,CD=2,梯形ABCD的面积为6,求平面α与底面ABCD所成二面角的大小.
【答案】
(1)证明:∵四棱柱ABCD﹣A1B1C1D1中,四边形ABCD为梯形,AD∥BC,
∴平面QBC∥平面A1D1DA,
∴平面A1CD与面QBC、平面A1D1DA的交线平行,∴QC∥A1D
∴△QBC∽△A1AD,
∴ ![]() =
= ![]() ,
,
∴Q为BB1的中点;
(2)解:连接QA,QD,设AA1=h,梯形ABCD的高为d,四棱柱被平面α所分成上、下两部分的体积为V1,V2,
设BC=a,则AD=2a,∴ ![]() =
= ![]() =
= ![]() ,VQ﹣ABCD=
,VQ﹣ABCD= ![]() =
= ![]() ahd,
ahd,
∴V2= ![]() ,
,
∵V棱柱= ![]() ahd,
ahd,
∴V1= ![]() ahd,
ahd,
∴四棱柱被平面α所分成上、下两部分的体积之比 ![]() ;
;
(3)解:在△ADC中,作AE⊥DC,垂足为E,连接A1E,则DE⊥平面AEA1,∴DE⊥A1E,
∴∠AEA1为平面α与底面ABCD所成二面角的平面角,
∵BC∥AD,AD=2BC,
∴S△ADC=2S△ABC,
∵梯形ABCD的面积为6,DC=2,
∴S△ADC=4,AE=4,
∴tan∠AEA1= ![]() =1,
=1,
∴∠AEA1= ![]() ,
,
∴平面α与底面ABCD所成二面角的大小为 ![]() .
.
【解析】(1)证明平面QBC∥平面A1D1DA,可得△QBC∽△A1AD,即可证明Q为BB1的中点;(2)设BC=a,则AD=2a,则 ![]() =
= ![]() =
= ![]() ,VQ﹣ABCD=
,VQ﹣ABCD= ![]() =
= ![]() ahd,利用V棱柱=
ahd,利用V棱柱= ![]() ahd,即可求出此四棱柱被平面α所分成上、下两部分的体积之比;(3)△ADC中,作AE⊥DC,垂足为E,连接A1E,则DE⊥平面AEA1 , DE⊥A1E,可得∠AEA1为平面α与底面ABCD所成二面角,求出S△ADC=4,AE=4,可得tan∠AEA1=
ahd,即可求出此四棱柱被平面α所分成上、下两部分的体积之比;(3)△ADC中,作AE⊥DC,垂足为E,连接A1E,则DE⊥平面AEA1 , DE⊥A1E,可得∠AEA1为平面α与底面ABCD所成二面角,求出S△ADC=4,AE=4,可得tan∠AEA1= ![]() =1,即可求平面α与底面ABCD所成二面角的大小.
=1,即可求平面α与底面ABCD所成二面角的大小.


科目:高中数学 来源: 题型:
【题目】为回馈顾客,某商场拟通过摸球兑奖的方式对1000位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元,求:
①顾客所获的奖励额为60元的概率;
②顾客所获的奖励额的分布列及数学期望;
(2)商场对奖励总额的预算是60000元,并规定袋中的4个球只能由标有面值10元和50元的两种球组成,或标有面值20元和40元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请对袋中的4个球的面值给出一个合适的设计,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 总计 | |
男性市民 |
| ||
女性市民 |
| ||
总计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过![]() 的前提下认为支持申办
的前提下认为支持申办![]() 年足球世界杯与性别有关?请说明理由.
年足球世界杯与性别有关?请说明理由.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=1+(1+a)x﹣x2﹣x3 , 其中a>0.
(1)讨论f(x)在其定义域上的单调性;
(2)当x∈[0,1]时,求f(x)取得最大值和最小值时的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线![]() 是一条居民平时散步的小道,小道两旁是空地,当地政府为了丰富居民的业余生活,要在小道两旁规划出两地来修建休闲活动场所,已知空地
是一条居民平时散步的小道,小道两旁是空地,当地政府为了丰富居民的业余生活,要在小道两旁规划出两地来修建休闲活动场所,已知空地![]() 和规划的两块用地(阴影区域)都是矩形,
和规划的两块用地(阴影区域)都是矩形,![]() ,
,![]() ,
,![]() ,若以
,若以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 为原点,建立如图平面直角坐标系,则曲线
为原点,建立如图平面直角坐标系,则曲线![]() 的方程为
的方程为![]() ,记
,记![]() ,规划的两块用地的面积之和为
,规划的两块用地的面积之和为![]() .(单位:)
.(单位:)

(1)求![]() 关于
关于![]() 的函数
的函数![]() ;
;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于O、A、B三点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为
=1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于O、A、B三点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为 ![]() ,则p=( )
,则p=( )
A.1
B.![]()
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com