分析:(I)根据异面直线所成角的定义,∠ABE为异面直线所成的角,再通过解三角形ABE可求.
(II)设AB
1∩A
1B=O,取C
1D
1中点F,连接OE、EB、B
1F.根据三角形中位线定理,得EF∥C
1D且EF=
C
1D,平行四边形AB
1C
1D中,有B
1O∥C
1D且B
1O=
C
1D,从而得到EF∥B
1O且EF=B
1O,四边形B
1OEF为平行四边形,B
1F∥OE,所以B
1F∥平面A
1BE,即存在C
1D
1中点F,使B
1F∥平面A
1BE.
解答: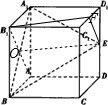
解:(1)在正方体ABCD-A
1B
1C
1D
1中,由于AB∥CD,
故∠ABE(或其补角)即为直线BE和直线CD所成角.
设正方体的棱长为1,则由E是棱DD
1的中点,可得AB=1,BE=
=
,
在Rt△ABE中,由余弦定理求得cos∠ABE=
=
.
(II)设AB
1∩A
1B=O,取C
1D
1中点F,连接OE、EB、B
1F.根据三角形中位线定理,得EF∥C
1D且EF=
C
1D,平行四边形AB
1C
1D中,有B
1O∥C
1D且B
1O=
C
1D,
∴EF∥B
1O且EF=B
1O,四边形B
1OEF为平行四边形,B
1F∥OE,又B
1F?平面A
1BE,OE?平面A
1BE,
∴B
1F∥平面A
1BE,
即存在C
1D
1中点F,使B
1F∥平面A
1BE.
点评:本题考查了异面直线所成的角,考查线面平行的判定及空间想象能力、推理论证能力.另外本题也可利用空间向量法求解.

 如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点. 解:(1)在正方体ABCD-A1B1C1D1中,由于AB∥CD,
解:(1)在正方体ABCD-A1B1C1D1中,由于AB∥CD,

 阅读快车系列答案
阅读快车系列答案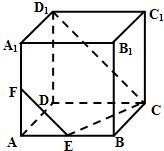 如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点
如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点 (2011•宝山区二模)如图所示,在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等,则动点P所在曲线形状为( )
(2011•宝山区二模)如图所示,在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等,则动点P所在曲线形状为( )