
| A. | 0 | B. | 1 | C. | 2 | D. | 0或2 |
分析 由等比数列性质得b=2q,a=2q2,从而方程$a{x^2}+bx+\frac{1}{3}=0$转化为:2q2x2+2qx+$\frac{1}{3}$=0,由此利用根的判别式能求出方程$a{x^2}+bx+\frac{1}{3}=0$的实根个数.
解答 解:∵实数2,b,a依次成等比数列,
∴b=2q,a=2q2
∴方程$a{x^2}+bx+\frac{1}{3}=0$转化为:2q2x2+2qx+$\frac{1}{3}$=0,
∵$△=(2q)^{2}-\frac{8}{3}{q}^{2}$=$\frac{4}{3}{q}^{2}$>0,
∴方程$a{x^2}+bx+\frac{1}{3}=0$的实根个数为2个.
故选:C.
点评 本题考查方程的实根个数的判断,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:解答题
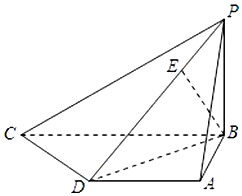 已知四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且BE⊥PD.
已知四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且BE⊥PD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
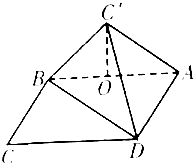 如图.在矩形ABCD中.AB=3 $\sqrt{3}$,BC=3,沿对角线BD把△BCD折起.使C移到C′.且C′在面ABC内的射影O恰好落在AB上.
如图.在矩形ABCD中.AB=3 $\sqrt{3}$,BC=3,沿对角线BD把△BCD折起.使C移到C′.且C′在面ABC内的射影O恰好落在AB上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | (0,1] | C. | [1,+∞) | D. | $[{\frac{1}{2},1}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3] | B. | (-1,3) | C. | [-3,1) | D. | [-3,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com