
【题目】平面直角坐标系xOy中,已知椭圆C:![]() 1(a>b>0)的离心率为
1(a>b>0)的离心率为![]() ,左右焦点分别是F1,F2,以F1为圆心,以3为半径的圆与以F2为圆心,以1为半径的圆相交,且交点
,左右焦点分别是F1,F2,以F1为圆心,以3为半径的圆与以F2为圆心,以1为半径的圆相交,且交点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)设椭圆E:![]() 1,P为椭圆C上任意一点,过点P的直线y=kx+m交椭圆E于A,B两点.射线PO交椭圆E于点Q.
1,P为椭圆C上任意一点,过点P的直线y=kx+m交椭圆E于A,B两点.射线PO交椭圆E于点Q.
(i)求![]() 的值,
的值,
(ii)求△ABQ面积的最大值.
【答案】(1)![]() 1(2)(i)|
1(2)(i)|![]() |=2,(ii)18
|=2,(ii)18
【解析】
(1)由MF1+MF2=2a=3+1=4以及![]() ,解方程组可得
,解方程组可得![]() ,由此可得椭圆C的方程;
,由此可得椭圆C的方程;
(2)(i) 设P(x0,y0),|![]() |=λ,可得Q(﹣λx0,﹣λy0),将其代入椭圆
|=λ,可得Q(﹣λx0,﹣λy0),将其代入椭圆![]() 的方程可得结果;
的方程可得结果;
(ii) 设A(x1,y1),B(x2,y2),将直线y=kx+m代入椭圆E的方程,利用韦达定理可得|x1﹣x2|![]() ,利用S
,利用S![]() |m||x1﹣x2|可得
|m||x1﹣x2|可得![]()
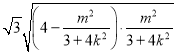 ,根据两个判别式大于0,可得
,根据两个判别式大于0,可得![]()
![]() ,再利用二次函数的单调性可得结果.
,再利用二次函数的单调性可得结果.
(1)由题意可知,MF1+MF2=2a=3+1=4,可得a=2,
又![]() ,a2﹣c2=b2,
,a2﹣c2=b2,
可得c=1,b![]() ,即有椭圆C的方程为
,即有椭圆C的方程为![]() 1;
1;
(2)由(1)知椭圆E的方程为![]() 1,
1,
(i)设P(x0,y0),|![]() |=λ,由题意可知,
|=λ,由题意可知,
Q(﹣λx0,﹣λy0),由于![]() 1,
1,
又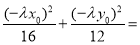 1,即
1,即![]() (
(![]() )=1,
)=1,
所以λ=2,即|![]() |=2;
|=2;
(ii)设A(x1,y1),B(x2,y2),将直线y=kx+m代入椭圆E的方程,可得
(3+4k2)x2+8kmx+4m2﹣48=0,由△>0,可得m2<12+16k2,①
则有x1+x2![]() ,x1x2
,x1x2![]() ,
,
所以|x1﹣x2|![]() ,
,
由直线y=kx+m与y轴交于(0,m),
则△AOB的面积为S![]() |m||x1﹣x2|
|m||x1﹣x2|![]() |m|
|m|![]()
=2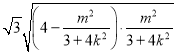 ,设
,设![]() t,则S=2
t,则S=2![]() ,
,
将直线y=kx+m代入椭圆C的方程,可得(3+4k2)x2+8kmx+4m2﹣12=0,
由△≥0可得m2≤3+4k2,②
由①②可得0<t≤1,则S=2![]() 在(0,1]递增,即有t=1取得最大值,
在(0,1]递增,即有t=1取得最大值,
即有S≤6,即m2=3+4k2时,![]() 取得最大值6,
取得最大值6,
由(i)知,△ABQ的面积为3S,
即△ABQ面积的最大值为18.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:
【题目】选修4— 4:坐标系与参数方程
设极坐标系与直角坐标系![]() 有相同的长度单位,原点
有相同的长度单位,原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,曲线
轴正半轴为极轴,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数),直线
是参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的参数方程;
的参数方程;
(Ⅱ)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值﹒
的值﹒
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】与正方体ABCD—A1B1C1D1的三条棱AB、CC1、A1D1所在直线的距离相等的点( )
A.有且只有1个B.有且只有2个
C.有且只有3个D.有无数个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两家公司都需要招聘求职者,这两家公司的聘用信息如下:
甲公司 | 乙公司 | |||||||||
职位 | A | B | C | D | 职位 | A | B | C | D | |
月薪/元 | 6000 | 7000 | 8000 | 9000 | 月薪/元 | 5000 | 7000 | 9000 | 11000 | |
获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 | 获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 | |
(1)根据以上信息,如果你是该求职者,你会选择哪一家公司?说明理由;
(2)某课外实习作业小组调查了1000名职场人士,就选择这两家公司的意愿做了统计,得到以下数据分布:
选择意愿 人员结构 | 40岁以上(含40岁)男性 | 40岁以上(含40岁)女性 | 40岁以下男性 | 40岁以下女性 |
选择甲公司 | 110 | 120 | 140 | 80 |
选择乙公司 | 150 | 90 | 200 | 110 |
若分析选择意愿与年龄这两个分类变量,计算得到的K2的观测值为k1=5.5513,测得出“选择意愿与年龄有关系”的结论犯错误的概率的上限是多少?并用统计学知识分析,选择意愿与年龄变量和性别变量哪一个关联性更大?
附:![]()
| 0.050 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C:x2+y2+4x-2y+m=0与直线![]() 相切.
相切.
(1)求圆C的方程;
(2)若圆C上有两点M,N关于直线x+2y=0对称,且![]() ,求直线MN的方程.
,求直线MN的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三个村庄A,B,C构成一个三角形,且AB=5千米,BC=12千米,AC=13千米.为了方便市民生活,现在△ABC内任取一点M建一大型生活超市,则M到A,B,C的距离都不小于2千米的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为梯形,![]() ,
,![]() ,
,![]() ,
,![]() 平面ABCD.
平面ABCD.
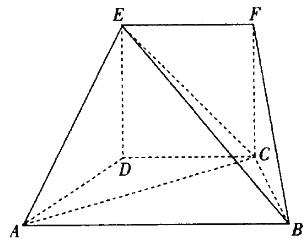
![]() 求BE与平面EAC所成角的正弦值;
求BE与平面EAC所成角的正弦值;
![]() 线段BE上是否存在点M,使平面
线段BE上是否存在点M,使平面![]() 平面DFM?若存在,求
平面DFM?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com