
分析 列出函数f(x)=x3-x-1在区间[1,1.5]内的一个零点附近曲函数值用二分法逐次计算表,由图中参考数据可得f(1.375)>0,f(1.3125)<0,又因为题中要求精确到0.1可得答案.
解答 解:函数f(x)=x3-x-1在区间[1,1.5]内的一个零点附近曲函数值用二分法逐次计算列表如下
| x | 1 | 1.5 | 1.25 | 1.375 | 1.3125 |
| f(x) | -1 | 0.875 | -0.2969 | 0.2246 | -0.05151 |
点评 本题本题主要考查用二分法求区间根的问题,属于基础题型.在利用二分法求区间根的问题上,如果题中有根的精确度的限制,在解题时就一定要计算到满足要求才能结束.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$) | B. | $\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{c}$-$\overrightarrow{b}$) | C. | $\frac{1}{2}$($\overrightarrow{b}$+$\overrightarrow{c}$-$\overrightarrow{a}$) | D. | $\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广西陆川县中学高二理9月月考数学试卷(解析版) 题型:解答题
已知二次函数 (
( ).
).
(1)若不等式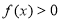 的解集为
的解集为 或
或 ,求
,求 和
和 的值;
的值;
(2)若 .
.
①解关于 的不等式
的不等式 ;
;
②若对任意 ,
,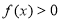 恒成立,求
恒成立,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com