
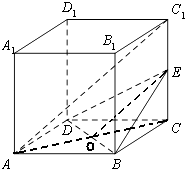
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E是棱CC1的中点. 
(1)证明:AC1∥平面BDE;
(2)证明:AC1⊥BD.
【答案】
(1)证明:连接AC交BD于O,连接OE,
∵ABCD是正方形,
∴O为AC的中点,
∵E是棱CC1的中点,
∴AC1∥OE.
又∵AC1平面BDE,OE平面BDE,
∴AC1∥平面BDE
(2)证明:
∵ABCD是正方形,
∴AC⊥BD.
∵CC1⊥平面ABCD,且BD平面ABCD,
∴CC1⊥BD.
又∵CC1∩AC=C,
∴BD⊥平面ACC1.
又∵AC1平面ACC1,
∴AC1⊥BD.
【解析】(1)根据线面平行的判定定理证明:AC1∥平面BDE;(2)根据线面垂直的性质,先证明BD⊥平面ACC1 , 然后证明AC1⊥BD.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对直线与平面垂直的性质的理解,了解垂直于同一个平面的两条直线平行.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知![]()
(1)若![]() ,且函数
,且函数![]() 在区间
在区间![]() 上单调递增,求实数a的范围;
上单调递增,求实数a的范围;
(2)若函数![]() 有两个极值点
有两个极值点![]() ,
, ![]() 且存在
且存在![]() 满足
满足![]() ,令函数
,令函数![]() ,试判断
,试判断![]() 零点的个数并证明.
零点的个数并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点. 
(1)证明:EF∥面PAD;
(2)证明:面PDC⊥面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
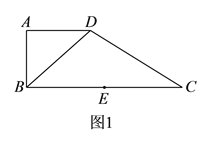
【题目】如图![]() ,在直角梯形
,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,得到如图
,得到如图![]() 所示的几何体.
所示的几何体.
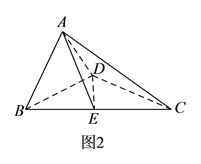
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,
, ![]() 与其在平面
与其在平面![]() 内的正投影所成角的正切值为
内的正投影所成角的正切值为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】田忌和齐王赛马是历史上有名的故事,设齐王的三匹马分别为A、B、C,田忌的三匹马分别为a、b、c.三匹马各比赛一次,胜两场者为获胜.若这六匹马比赛的优劣程度可以用以下不等式表示:A>a>B>b>C>c. (Ⅰ)如果双方均不知道对方马的出场顺序,求田忌获胜的概率;
(Ⅱ)为了得到更大的获胜概率,田忌预先派出探子到齐王处打探实情,得知齐王第一场必出上等马.那么,田忌应怎样安排出马的顺序,才能使自己获胜的概率最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com