
【题目】如图,圆O是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中A,B两点在⊙O上,A,B,C,D恰是一个正方形的四个顶点.根据规划要求,在A,B,C,D四点处安装四盏照明设备,从圆心O点出发,在地下铺设4条到A,B,C,D四点线路OA,OB,OC,OD.
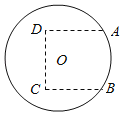
(1)若正方形边长为10米,求广场的面积;
(2)求铺设的4条线路OA,OB,OC,OD总长度的最小值.
【答案】(1)100![]() (平方米)(2)
(平方米)(2)![]() (米)
(米)
【解析】
(1)连接AB,广场面积等于正方形面积加上弓形面积,计算得到答案.
(2)过O作OK⊥CD,垂足为K,过O作OH⊥AD(或其延长线),垂足为H,设∠OAD=θ(0<θ![]() ),OD
),OD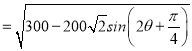 ,计算得到答案.
,计算得到答案.
(1)连接AB,∵AB=10,∴正方形ABCD的面积为100,
又OA=OB=10,∴△AOB为正三角形,则![]() ,
,
而圆的面积为100π,∴扇形AOB的面积为![]() ,
,
又三角形AOB的面积为![]() .∴弓形面积为
.∴弓形面积为![]() ,
,
则广场面积为100![]() (平方米);
(平方米);
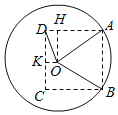
(2)过O作OK⊥CD,垂足为K,过O作OH⊥AD(或其延长线),垂足为H,
设∠OAD=θ(0<θ![]() ),则OH=10sinθ,AH=10cosθ,
),则OH=10sinθ,AH=10cosθ,
∴DH=|AD﹣AH|=|2OH﹣AH|=|20sinθ﹣10cosθ|,
∴OD .
.
∴当θ![]() 时,
时,![]() .
.
∴4条线路OA,OB,OC,OD总长度的最小值为![]()
![]() (米).
(米).


科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD是边长为2的菱形,∠ABC=60°,平面AEFC⊥平面ABCD,EF∥AC,AE=AB,AC=2EF.
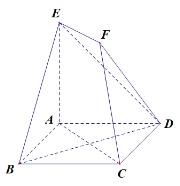
(1)求证:平面BED⊥平面AEFC;
(2)若四边形AEFC为直角梯形,且EA⊥AC,求二面角B-FC-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,且曲线
轴的正半轴为极轴建立极坐标系,且曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 上的定点
上的定点![]() 在曲线
在曲线![]() 外且其到
外且其到![]() 上的点的最短距离为
上的点的最短距离为![]() ,试求点
,试求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点![]() 在正视图上的对应点为
在正视图上的对应点为![]() ,圆柱表面上的点
,圆柱表面上的点![]() 在左视图上的对应点为
在左视图上的对应点为![]() ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从![]() 到
到![]() 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为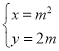 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(Ⅱ)已知点![]() 设直线
设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求直线
,求直线![]() 与曲线
与曲线![]() 的交点的直角坐标;
的交点的直角坐标;
(2)若点![]() 在曲线
在曲线![]() 上,且
上,且![]() 到直线
到直线![]() 距离的最大值为
距离的最大值为![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com