
ЁОЬтФПЁПШчЭМЪЧКЏЪ§yЃНAsin(ІиxЃЋІе)( ![]() ЃЌ
ЃЌ ![]() )ЭМ
)ЭМ
ЯёЕФвЛВПЗж.ЮЊСЫЕУЕНетИіКЏЪ§ЕФЭМЯёЃЌжЛвЊНЋyЃНsin x(xЁЪR)ЕФЭМЯёЩЯЫљгаЕФЕу( )
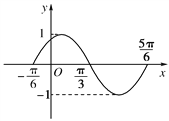
A. ЯђзѓЦНвЦ![]() ИіЕЅЮЛГЄЖШЃЌдйАбЫљЕУИїЕуЕФКсзјБъЫѕЖЬЕНдРДЕФ
ИіЕЅЮЛГЄЖШЃЌдйАбЫљЕУИїЕуЕФКсзјБъЫѕЖЬЕНдРДЕФ![]() ЃЌзнзјБъВЛБф.
ЃЌзнзјБъВЛБф.
B. ЯђзѓЦНвЦ![]() ИіЕЅЮЛГЄЖШЃЌдйАбЫљЕУИїЕуЕФКсзјБъЩьГЄЕНдРДЕФ2БЖЃЌзнзјБъВЛБф.
ИіЕЅЮЛГЄЖШЃЌдйАбЫљЕУИїЕуЕФКсзјБъЩьГЄЕНдРДЕФ2БЖЃЌзнзјБъВЛБф.
C. ЯђзѓЦНвЦ![]() ИіЕЅЮЛГЄЖШЃЌдйАбЫљЕУИїЕуЕФКсзјБъЫѕЖЬЕНдРДЕФ
ИіЕЅЮЛГЄЖШЃЌдйАбЫљЕУИїЕуЕФКсзјБъЫѕЖЬЕНдРДЕФ![]() ЃЌзнзјБъВЛБф.
ЃЌзнзјБъВЛБф.
D. ЯђзѓЦНвЦ![]() ИіЕЅЮЛГЄЖШЃЌдйАбЫљЕУИїЕуЕФКсзјБъЩьГЄЕНдРДЕФ2БЖЃЌзнзјБъВЛБф.
ИіЕЅЮЛГЄЖШЃЌдйАбЫљЕУИїЕуЕФКсзјБъЩьГЄЕНдРДЕФ2БЖЃЌзнзјБъВЛБф.
ЁОД№АИЁПA
ЁОНтЮіЁПКмУїЯд![]() ЃЌ
ЃЌ
НсКЯКЏЪ§ЕФЭМЯѓПЩЕУЃК ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЌ
ЃЌ
Сю![]() ПЩЕУЃК
ПЩЕУЃК ![]() ЃЌ
ЃЌ
ЙЪШ§НЧКЏЪ§ЕФНтЮіЪНЮЊЃК ![]() ЃЌ
ЃЌ
ОнДЫПЩжЊЃЌвЊЕУЕНДЫКЏЪ§ЕФЭМЯѓЃЌ
жЛашНЋyЃНsin x(xЁЪR)ЕФЭМЯёЩЯЫљгаЕФЕуЯђзѓЦНвЦ![]() ИіЕЅЮЛГЄЖШЃЌ
ИіЕЅЮЛГЄЖШЃЌ
дйАбЫљЕУИїЕуЕФКсзјБъЫѕЖЬЕНдРДЕФ![]() ЃЌзнзјБъВЛБф.
ЃЌзнзјБъВЛБф.
БОЬтбЁдёAбЁЯю.
ЕуОІЖдгкШ§НЧКЏЪ§ЭМЯѓЕФЦНвЦБфЛЛЮЪЬтЃЌЦфЦНвЦБфЛЛЙцдђЪЧЁАзѓМгЁЂгвМѕЁБЃЌВЂЧвдкБфЛЛЙ§ГЬжажЛБфЛЛЦфжаЕФздБфСПxЃЌШчЙћxЕФЯЕЪ§ВЛЪЧ1ЃЌОЭвЊАбетИіЯЕЪ§ЬсШЁКѓдйШЗЖЈБфЛЛЕФЕЅЮЛКЭЗНЯђЃЎСэЭтЃЌЕБСНИіКЏЪ§ЕФУћГЦВЛЭЌЪБЃЌЪзЯШвЊНЋКЏЪ§УћГЦЭГвЛЃЌЦфДЮвЊАбІиxЃЋІеБфЛЛГЩ![]() ЃЌзюКѓШЗЖЈЦНвЦЕФЕЅЮЛВЂИљОн
ЃЌзюКѓШЗЖЈЦНвЦЕФЕЅЮЛВЂИљОн![]() ЕФЗћКХШЗЖЈЦНвЦЕФЗНЯђЃЎ
ЕФЗћКХШЗЖЈЦНвЦЕФЗНЯђЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкШ§Ртжљ![]() жаЃЌЦНУц
жаЃЌЦНУц![]() ЕзУц
ЕзУц![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌВрРт
ЕФжаЕуЃЌВрРт![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФгрЯвжЕЃЎ
ЫљГЩНЧЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
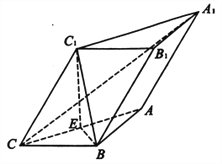
ЁОЬтФПЁПЭМ1ЃЌЦНааЫФБпаЮ![]() жаЃЌ
жаЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЯжНЋ
ЃЌЯжНЋ![]() би
би![]() елЦ№ЃЌЕУЕНШ§РтзЖ
елЦ№ЃЌЕУЕНШ§РтзЖ![]() ЃЈШчЭМ2ЃЉЃЌЧв
ЃЈШчЭМ2ЃЉЃЌЧв![]() ЃЌЕу
ЃЌЕу![]() ЮЊВрРт
ЮЊВрРт![]() ЕФжаЕу.
ЕФжаЕу.
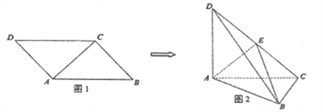
ЃЈ1ЃЉЧѓжЄЃК ![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓШ§РтзЖ![]() ЕФЬхЛ§ЃЛ
ЕФЬхЛ§ЃЛ
ЃЈ3ЃЉдк![]() ЕФНЧЦНЗжЯпЩЯЪЧЗёДцдкЕу
ЕФНЧЦНЗжЯпЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЦНУц
ЦНУц![]() ЃПШєДцдкЃЌЧѓ
ЃПШєДцдкЃЌЧѓ![]() ЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшШЋМЏU=RЃЌМЏКЯA={x|Љ1ЁмxЃМ3}ЃЌB={x|2xЉ4ЁнxЉ2}ЃЎ
ЃЈ1ЃЉЧѓUЃЈAЁЩBЃЉЃЛ
ЃЈ2ЃЉШєМЏКЯC={x|2x+aЃО0}ЃЌТњзуBЁШC=CЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
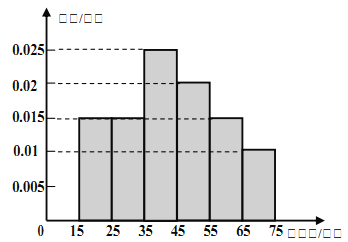
ЁОЬтФПЁП2016Фъ5дТ20ШеЃЌеыЖдВПЗжЁАЖўЯпГЧЪаЁБЗПМлЩЯеЧЙ§ПьЃЌУНЬхШЯЮЊЙњЮёдКГЃЮёЛсвщПЩФмдйДЮШЗЖЈЮхЬѕДыЪЉ(МђГЦЁАЙњЮхЬѕЁБ).ЮЊДЫЃЌМЧепЖдФГГЧЪаЕФЙЄаННзВуЙигкЁАЙњЮхЬѕЁБЬЌЖШНјааСЫЕїВщЃЌЫцЛњГщШЁСЫ![]() ШЫЃЌзїГіСЫЫћУЧЕФдТЪеШыЕФЦЕТЪЗжВМжБЗНЭМ(ШчЭМ)ЃЌЭЌЪБЕУЕНСЫЫћУЧЕФдТЪеШыЧщПігыЁАЙњЮхЬѕЁБдоГЩШЫЪ§ЭГМЦБэ(ШчЯТБэ):
ШЫЃЌзїГіСЫЫћУЧЕФдТЪеШыЕФЦЕТЪЗжВМжБЗНЭМ(ШчЭМ)ЃЌЭЌЪБЕУЕНСЫЫћУЧЕФдТЪеШыЧщПігыЁАЙњЮхЬѕЁБдоГЩШЫЪ§ЭГМЦБэ(ШчЯТБэ):
дТЪеШыЃЈАйдЊЃЉ | доГЩШЫЪ§ |
|
|
|
|
|
|
|
|
|
|
|
|
ЃЈ1ЃЉЪдИљОнЦЕТЪЗжВМжБЗНЭМЙРМЦет![]() ШЫЕФжаЮЛЪ§КЭЦНОљдТЪеШыЃЛ
ШЫЕФжаЮЛЪ§КЭЦНОљдТЪеШыЃЛ
ЃЈ2ЃЉШєДгдТЪеШы(ЕЅЮЛ:АйдЊ)дк![]() ЕФБЛЕїВщепжаЫцЛњбЁШЁ
ЕФБЛЕїВщепжаЫцЛњбЁШЁ![]() ШЫНјаазЗзйЕїВщЃЌЧѓБЛбЁШЁЕФ
ШЫНјаазЗзйЕїВщЃЌЧѓБЛбЁШЁЕФ![]() ШЫЖМВЛдоГЩЕФИХТЪ.
ШЫЖМВЛдоГЩЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЩшЭждВЕФжааФЮЊдЕу![]() ЃЌГЄжсдк
ЃЌГЄжсдк![]() жсЩЯЃЌЩЯЖЅЕуЮЊ
жсЩЯЃЌЩЯЖЅЕуЮЊ![]() ЃЌзѓЃЌгвНЙЕуЗжБ№ЮЊ
ЃЌзѓЃЌгвНЙЕуЗжБ№ЮЊ![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЕФжаЕуЗжБ№ЮЊ
ЕФжаЕуЗжБ№ЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЪЧУцЛ§ЮЊ4ЕФжБНЧШ§НЧаЮ.
ЪЧУцЛ§ЮЊ4ЕФжБНЧШ§НЧаЮ.
ЃЈ1ЃЉЧѓИУЭждВЕФРыаФТЪКЭБъзМЗНГЬЃЛ
ЃЈ2ЃЉЙ§![]() зіжБЯп
зіжБЯп![]() НЛЭждВгк
НЛЭждВгк![]() СНЕуЃЌЪЙ
СНЕуЃЌЪЙ![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЕФЗНГЬ.
ЕФЗНГЬ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФРтзЖ![]() ЃЌЕзУц
ЃЌЕзУц![]() ЪЧБпГЄЮЊ2ЕФСтаЮЃЌ
ЪЧБпГЄЮЊ2ЕФСтаЮЃЌ ![]() ЃЌЧв
ЃЌЧв![]() ЦНУц
ЦНУц![]() .
.

ЃЈ1ЃЉжЄУїЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЦНУц![]() гыЦНУц
гыЦНУц![]() ЕФМаНЧЮЊ
ЕФМаНЧЮЊ![]() ЃЌЪдЧѓЯпЖЮ
ЃЌЪдЧѓЯпЖЮ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЂёЃЉЩшВЛЕШЪН![]() ЖдТњзу
ЖдТњзу![]() ЕФвЛЧаЪЕЪ§
ЕФвЛЧаЪЕЪ§![]() ЕФШЁжЕЖМГЩСЂЃЌЧѓ
ЕФШЁжЕЖМГЩСЂЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈЂђЃЉЪЧЗёДцдкЪЕЪ§![]() ,ЪЙЕУВЛЕШЪН
,ЪЙЕУВЛЕШЪН![]() ЖдТњзу
ЖдТњзу![]() ЕФвЛЧаЪЕЪ§
ЕФвЛЧаЪЕЪ§![]() ЕФШЁжЕЖМГЩСЂЃЎ
ЕФШЁжЕЖМГЩСЂЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвдЕуCЃЈtЃЌ![]() ЃЉ ЃЈtЁЪRЃЌtЁй0ЃЉЮЊдВаФЕФдВгыxжсНЛгкЕуOЁЂAЃЌгыyжсНЛгкЕуOЁЂBЃЌЦфжаOЮЊдЕуЃЎ
ЃЉ ЃЈtЁЪRЃЌtЁй0ЃЉЮЊдВаФЕФдВгыxжсНЛгкЕуOЁЂAЃЌгыyжсНЛгкЕуOЁЂBЃЌЦфжаOЮЊдЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAOBЕФУцЛ§ЮЊЖЈжЕЃЛ
ЃЈ2ЃЉЩшжБЯп2x+yЉ4=0гыдВCНЛгкЕуMЁЂNЃЌШєOM=ONЃЌЧѓдВCЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com