
【题目】设函数![]() ,
,![]() .
.
(1)若![]() ,且
,且![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 且
且![]() ,求证:
,求证:![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析: (1)已知单调区间求参数的取值范围,将问题转化为函数的最值问题;
(2)研究函数的零点,用零点存在性定理、数形结合思想求解.
试题解析:(1)∵![]() ,∴
,∴![]() ,
,
若![]() ,且
,且![]() 在区间
在区间![]() 上单调递增,
上单调递增,
则![]() 对任意的
对任意的![]() 恒成立,即
恒成立,即![]() 对任意的
对任意的![]() 恒成立,
恒成立,
∴![]() ,即实数
,即实数![]() 的取值范围为
的取值范围为![]() .
.
(2)当![]() 时,
时,![]() ,∴
,∴![]() ,
,
由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() .∴
.∴![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,且
上单调递减,且![]() ,
,
∴![]() 在区间
在区间![]() 上有且仅有一个零点,
上有且仅有一个零点,
当![]() 时,
时,![]() ,∴
,∴![]() 在区间
在区间![]() 上单调递减,
上单调递减,
又![]() ,
,![]() ,
,
∴![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
综上,若![]() 且
且![]() ,则
,则![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
点晴:本题主要考查的是利用导数研究函数的单调性以及零点的个数,对逻辑思维能力、数形结合思想要求很高,属于难题.第(1)问已知单调区间求参数的取值范围,将含参函数问题转化为确定函数的最值问题;第(2)问研究函数的零点,用零点存在性定理、数形结合思想求解.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益
,乙城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元)。
(单位:万元)。
(1)当甲城市投资50万元时,求此时公司总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥PABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC与BD交于点O,点E,F分别在AD,CD上,AE=CF,EF交BD于点H.将△DEF沿EF折到△D′EF的位置.
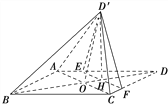
(1)证明:AC⊥HD′;
(2)若AB=5,AC=6,AE=![]() ,OD′=2
,OD′=2![]() ,求五棱锥D′ABCFE的体积.
,求五棱锥D′ABCFE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xln x-(x-1)(ax-a+1)(a∈R).
(1)若a=0,判断函数f(x)的单调性;
(2)若x>1时,f(x)<0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府鉴于某种日常食品价格增长过快,欲将这种食品价格控制在适当范围内,决定对这种食品生产厂家提供政府补贴,设这种食品的市场价格为x元/千克,政府补贴为t元/千克,根据市场调查,当16≤x≤24时,这种食品市场日供应量p万千克与市场日需求量q万千克近似地满足关系:p=2(x+4t-14)(x≥16,t≥0),q=24+8ln ![]() (16≤x≤24).当p=q时的市场价格称为市场平衡价格.
(16≤x≤24).当p=q时的市场价格称为市场平衡价格.
(1)将政府补贴表示为市场平衡价格的函数,并求出函数的值域.
(2)为使市场平衡价格不高于每千克20元,政府补贴至少为每千克多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com