
【题目】在△ABC中,内角A、B、C所对的边分别是a、b、c,且a+b+c=8.
(1)若a=2,b= ![]() ,求cosC的值;
,求cosC的值;
(2)若sinAcos2 ![]() +sinBcos2
+sinBcos2 ![]() =2sinC,且△ABC的面积S=
=2sinC,且△ABC的面积S= ![]() sinC,求a和b的值.
sinC,求a和b的值.
【答案】
(1)解:∵a=2,b= ![]() ,且a+b+c=8,
,且a+b+c=8,
∴c=8﹣(a+b)= ![]() ,
,
∴由余弦定理得:cosC= ![]() =
= 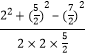 =﹣
=﹣ ![]() ;
;
(2)解:由sinAcos2 ![]() +sinBcos2
+sinBcos2 ![]() =2sinC可得:sinA
=2sinC可得:sinA ![]() +sinB
+sinB ![]() =2sinC,
=2sinC,
整理得:sinA+sinAcosB+sinB+sinBcosA=4sinC,
∵sinAcosB+cosAsinB=sin(A+B)=sinC,
∴sinA+sinB=3sinC,
利用正弦定理化简得:a+b=3c,
∵a+b+c=8,
∴a+b=6①,
∵S= ![]() absinC=
absinC= ![]() sinC,
sinC,
∴ab=9②,
联立①②解得:a=b=3.
【解析】(1)由a+b+c=8,根据a=2,b= ![]() 求出c的长,利用余弦定理表示出cosC,将三边长代入求出cosC的值即可;(2)已知等式左边利用二倍角的余弦函数公式化简,整理后利用两角和与差的正弦函数公式及诱导公式变形,再利用正弦定理得到a+b=3c,与a+b+c=8联立求出a+b的值,利用三角形的面积公式列出关系式,代入S=
求出c的长,利用余弦定理表示出cosC,将三边长代入求出cosC的值即可;(2)已知等式左边利用二倍角的余弦函数公式化简,整理后利用两角和与差的正弦函数公式及诱导公式变形,再利用正弦定理得到a+b=3c,与a+b+c=8联立求出a+b的值,利用三角形的面积公式列出关系式,代入S= ![]() sinC求出ab的值,联立即可求出a与b的值.
sinC求出ab的值,联立即可求出a与b的值.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】某校有一块圆心![]() ,半径为200米,圆心角为
,半径为200米,圆心角为![]() 的扇形绿地
的扇形绿地![]() ,半径
,半径![]() 的中点分别为
的中点分别为![]() ,
,![]() 为弧
为弧![]() 上的一点,设
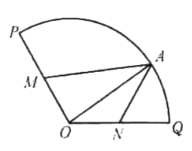
上的一点,设![]() ,如图所示,拟准备两套方案对该绿地再利用.
,如图所示,拟准备两套方案对该绿地再利用.
(1)方案一:将四边形绿地![]() 建成观赏鱼池,其面积记为
建成观赏鱼池,其面积记为![]() ,试将
,试将![]() 表示为关于
表示为关于![]() 的函数关系式,并求
的函数关系式,并求![]() 为何值时,
为何值时,![]() 取得最大?
取得最大?
(2)方案二:将弧![]() 和线段
和线段![]() 围成区域建成活动场地,其面积记为
围成区域建成活动场地,其面积记为![]() ,试将
,试将![]() 表示为关于
表示为关于![]() 的函数关系式;并求
的函数关系式;并求![]() 为何值时,
为何值时,![]() 取得最大?
取得最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+bx+1的图象经过点(1,﹣3)且在x=1处f(x)取得极值.求:
(1)函数f(x)的解析式;
(2)f(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程![]() ,变量
,变量![]() 增加一个单位时,
增加一个单位时,![]() 平均增加
平均增加![]() 个单位;
个单位;
③线性回归方程![]() 必过
必过![]() );
);
④在一个![]() 列联表中,由计算得
列联表中,由计算得![]() ,则有
,则有![]() 以上的把握认为这两个变量间有关系.
以上的把握认为这两个变量间有关系.
其中错误的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正三棱柱ABC=A1B1C1的各棱长都是4,E是BC的中点,动点F在侧棱CC1上,且不与点C重合.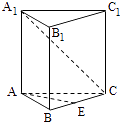
(1)当CF=1时,求证:EF⊥A1C;
(2)设二面角C﹣AF﹣E的大小为θ,求tanθ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为贯彻“激情工作,快乐数学”的理念,某学校在学习之余举行趣味知识有奖竞赛,比赛分初赛和决赛两部分,为了增加节目的趣味性,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰,已知选手甲答题的正确率为 ![]() .
.
(1)求选手甲答题次数不超过4次可进入决赛的概率;
(2)设选手甲在初赛中答题的个数ξ,试写出ξ的分布列,并求ξ的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=PA=4,A点在PD上的射影为G点,E点在AB上,平面PCE⊥平面PCD. 
(1)求证:AG⊥平面PCD;
(2)求直线PD与平面PCE所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com