
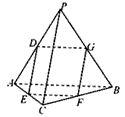
| (Ⅰ)证明:因为D,E分别为AP,AC的中点,所以DE//PC, 又因为DE 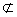 平面BCP, 平面BCP,所以DE//平面BCP。 (Ⅱ)证明:因为D,E,F,G分别为AP,AC,BC,PB的中点, 所以DE∥PC∥FG,DG∥AB∥EF, 所以四边形DEFG为平行四边形, 又因为PC⊥AB,所以DE⊥DG, 所以四边形DEFG为矩形。 |
|
| (Ⅲ)解:存在点Q满足条件,理由如下:连接DF,EG, 设Q为EG的中点,由(Ⅱ)知,DF∩EG=Q,且QD=QE=QF=QG=  EG, EG,分别取PC,AB的中点M,N,连接ME,EN,NG,MG,MN。 与(Ⅱ)同理,可证四边形MENG为矩形, 其对角线点为EG的中点Q,且QM=QN= 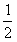 EG, EG,所以Q为满足条件的点。 |
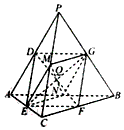 |


科目:高中数学 来源: 题型:
 (2012•广州一模)如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.
(2012•广州一模)如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求BC与平面PAB所成的角;
(2)求PC与平面ABC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省高三上学期期中考试文科数学试卷(解析版) 题型:解答题
(本小题满分14分)
如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA,AC、CB、BP的中点.

(1)求证:D、E、F、G四点共面;
(2)求证:PC⊥AB;
(3)若△ABC和△PAB都是等腰直角三角形,且AB=2,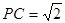 ,求四面体PABC的体积.
,求四面体PABC的体积.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省江门市高三(上)期末数学试卷(文科)(解析版) 题型:解答题
 如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.
如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点. ,求四面体PABC的体积.
,求四面体PABC的体积.查看答案和解析>>
科目:高中数学 来源:2012年广东省广州市高考数学一模调研交流试卷(文科)(解析版) 题型:解答题
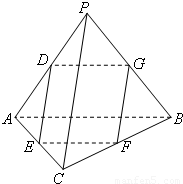 如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点.
如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA、AC、CB、BP的中点. ,求四面体PABC的体积.
,求四面体PABC的体积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com