
����Ŀ��ij���ս�ĿΪ��ǿ�����ԣ�Ҫ���ֳ��α����䳡����������������Ǿܾ����ݽ�Ŀ�ĺ��Ѿ������ߺ��ѵĻ������ѡ����ݽ�Ŀ�ĺ��Ѿ�������δ�μӹ��˻��3�����Ѳ���˻���Դ���ȥ��
������ÿ����ѡ���������ǵȿ��ܵģ��һ���Ӱ�죬��ij��ѡ����ݺ������ߵ�3�������в�����2������ѡ����ݽ�Ŀ�ĸ����Ƕ��٣�
����Ϊ���顰ѡ������ߡ������Ա��Ƿ��йأ���ȡ��������õ������
ѡ����� | �ܾ����� | �ϼ� | |
�� | 50 | 10 | 60 |
Ů | 10 | 10 | 20 |
�ϼ� | 60 | 20 | 80 |
�ٸ��ݱ������ݣ��Ƿ���99%�İ�����Ϊ�����ݽ�Ŀ������ѵ��Ա��йأ�
�ڽ���������Ƶ����Ϊ����ĸ��ʣ��������3�����Ժ��ѣ���XΪ3������ѡ����ݵ���������X�ķֲ��к�������
����K2= ![]() ��
��
P��K2��k0�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
���𰸡��⣺������3λ����ѡ����ݷֱ��ΪA��B��C���� ![]() ��
�� ![]() ��
�� ![]() �ֱ��ʾ��3λ���Ѿܾ����ݣ���3λ���Ѳ���û�Ŀ��ܽ��Ϊ{A��B��C}��{
�ֱ��ʾ��3λ���Ѿܾ����ݣ���3λ���Ѳ���û�Ŀ��ܽ��Ϊ{A��B��C}��{ ![]() ��B��C}��{A��
��B��C}��{A�� ![]() ��C}��{A��B��
��C}��{A��B�� ![]() }��{
}��{ ![]() ��
�� ![]() ��C}��{A��
��C}��{A�� ![]() ��
�� ![]() }��{
}��{ ![]() ��B��
��B�� ![]() }��{
}��{ ![]() ��
�� ![]() ��
�� ![]() }����8�֣�����3λ���Ѳ�����3λ����ѡ����ݵĿ��ܽ����4�֣����ݹŵ����ʽ���������ΪP=
}����8�֣�����3λ���Ѳ�����3λ����ѡ����ݵĿ��ܽ����4�֣����ݹŵ����ʽ���������ΪP= ![]() =
= ![]() ��
��
���ٸ���2��2���������õ�K2= ![]() ��8.9��6.635��������99%�İ�����Ϊ�����ݽ�Ŀ������ѵ��Ա��йأ�
��8.9��6.635��������99%�İ�����Ϊ�����ݽ�Ŀ������ѵ��Ա��йأ�
�������⣬ÿ������ѡ����ݵĸ���Ϊ ![]() ����X��B��3��
����X��B��3�� ![]() ����
����
�����������X�ĸ��ʷֲ���Ϊ��
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
���������X������ΪEX=3�� ![]() =
= ![]()
�����������������оٷ���ȷ�������¼��ĸ���������������ʣ����ٸ���2��2���������õ�K2= ![]() ��8.9��6.635�����ɵó����ۣ��������⣬ÿ������ѡ����ݵĸ���Ϊ
��8.9��6.635�����ɵó����ۣ��������⣬ÿ������ѡ����ݵĸ���Ϊ ![]() ����X��B��3��
����X��B��3�� ![]() �����ɵ�X�ķֲ��к�������
�����ɵ�X�ķֲ��к�������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ö�ʵؾ��ȵ�����,�������ϵĵ���֮�Ͳ�����5�ĸ��ʼ�Ϊp1,����֮�ʹ���5�ĸ��ʼ�Ϊp2,����֮��Ϊż���ĸ��ʼ�Ϊp3,��(����)
A. p1<p2<p3 B. p2<p1<p3
C. p1<p3<p2 D. p3<p1<p2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������EF��ABCD�У�ABCD�������Σ�AC��BD�ཻ��O��EF��AC����E��AC�ϵ���Ӱǡ�����߶�AO���е㣮
������֤��BD��ƽ��ACF��
������ֱ��AE��ƽ��ABCD���ɵĽ�Ϊ60�㣬��ƽ��DEF��ƽ��ABCD���ɽǵ�����ֵ��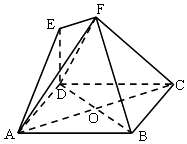
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ͼ�٣��ȱ�������ABC�ı߳�Ϊ2a��CD��AB���ϵĸߣ�E��F�ֱ���AC��BC���ϵĵ㣬������![]() ��k���ֽ���ABC��CD���۳�ֱ�����ADCB����ͼ��ͼ��.
��k���ֽ���ABC��CD���۳�ֱ�����ADCB����ͼ��ͼ��.
(1)���жϷ��ۺ�ֱ��AB��ƽ��DEF��λ�ù�ϵ����˵�����ɣ�
(2)������BACD������ֵ��
�� ������
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ͬѧ���ú��ٽ������ʵ�������![]() �����Ⱥ�����ȡ
�����Ⱥ�����ȡ![]() �˽�����һ������ϰ����
�˽�����һ������ϰ����
����ϵ�̼����ĵ��飬������ϰ�߷��ϵ�̼����ij�Ϊ����̼�����������Ϊ���ǵ�̼��������
������ͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��
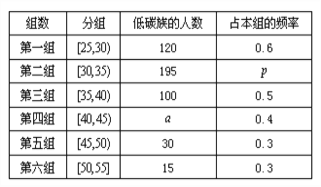
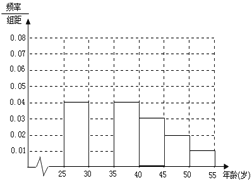
��I����ȫƵ�ʷֲ�ֱ��ͼ����![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
��II�����������![]() ������̼�����в��÷ֲ��������ȡ
������̼�����в��÷ֲ��������ȡ![]() �˲μӻ����̼����������ѡȡ
�˲μӻ����̼����������ѡȡ![]() ����Ϊ��ӣ���ѡȡ��
����Ϊ��ӣ���ѡȡ��![]() �������ǡ��1��������
�������ǡ��1��������![]() ��ĸ�����
��ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ũ��Ժ��ר��Ϊ���˽��������ļס�����������ij���������Ӽס�������������������и���ȡ6����������������ߣ��������£�(��λ��cm)
�ף�9,10,11,12,10,20
�ң�8,14,13,10,12,21.
(1)�ڸ����ķ����ڻ������ȡ�ļס�������������ߵľ�Ҷͼ��
(2)�ֱ��������ȡ�ļס�������������ߵ�ƽ�����뷽����ɴ��жϼס�����������ij��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������ܲ���Ϊ�˶Ըõ�����ʻԱ��ij��Գɼ����з����������ȡ��15�ֵ�45��֮���1000��ѧԱ�ijɼ�����������1000����ʻԱ�ijɼ�����������Ƶ�ʷֲ�ֱ��ͼ����ͼ������ɼ���[30��35���ڵļ�ʻԱ�������У� �� 
A.60
B.180
C.300
D.360
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��![]() ��
�� ![]() ��������
��������![]() ����
����![]() ��
�� ![]() ���㣬����������
���㣬����������![]() ��
�� ![]() ���㴦������
���㴦������![]() ��
�� ![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ��
��
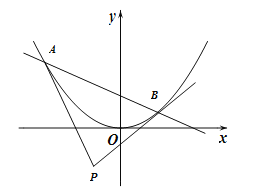
��I����֤: ![]() ��
��
��II�����![]() ������(��
������(��![]() ��
�� ![]() ��ʾ)��
��ʾ)��
��������![]() ������
������![]() ���������Сֵ��
���������Сֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com