
【题目】从甲、乙两种棉花中各抽测了25根棉花的纤维长度(单位: ![]() ) 组成一个样本,且将纤维长度超过315
) 组成一个样本,且将纤维长度超过315![]() 的棉花定为一级棉花.设计了如下茎叶图:
的棉花定为一级棉花.设计了如下茎叶图:

(1)根据以上茎叶图,对甲、乙两种棉花的纤维长度作比较,写出两个统计结论(不必计算);
(2)从样本中随机抽取甲、乙两种棉花各2根,求其中恰有3根一级棉花的概率;
(3)用样本估计总体,将样本频率视为概率,现从甲、乙两种棉花中各随机抽取1根,求其中一级棉花根数X的分布列及数学期望
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】分析:第一问根据题中所给的茎叶图中数据的分析,确定出哪种棉花的纤维平均长度大,从数据的集中程度来分析哪种棉花的纤维长度的分散程度大,排序之后找正中间的那个数就是中位数,分析数据的特征判断其是否对称,第二问用组合数求得对应的基本事件数,从而求得概率,第三问找到变量的可取值,求得其概率,列出分布列,利用公式求得其期望值.
详解:(1) 1.乙种棉花的纤维平均长度大于甲种棉花的纤维平均长度(或:乙种棉花的纤维长度普遍大于甲种棉花的纤维长度).
2.甲种棉花的纤维长度较乙种棉花的纤维长度更分散.(或:乙种棉花的纤维长度较甲种棉花的纤维长度更集中(稳定),甲种棉花的纤维长度的分散程度比乙种棉花的纤维长度的分散程度更大.)
3.甲种棉花的纤维长度的中位数为307![]() .乙种棉花的纤维长度的中位数为318
.乙种棉花的纤维长度的中位数为318![]() .
.
4.乙种棉花的纤维长度基本上是对称的,而且大多集中在中间(均值附近).甲种棉花的纤维长度除一个特殊值(352) 外,也大致对称,其分布较均匀.
(2) 记事件![]() 为“从样本中随机抽取甲、乙两种棉花各2根,其中恰有3根一级棉花”.
为“从样本中随机抽取甲、乙两种棉花各2根,其中恰有3根一级棉花”.
则![]()
![]()
![]()
(3) 由题意知,![]() 的可能取值是0,1,2,其相应的概率为
的可能取值是0,1,2,其相应的概率为
![]() ,
,![]()
![]() ,
,![]() ,
,
所以![]() 的分布列为
的分布列为
| 0 | 1 | 2 |
|
|
|
|
![]()
![]()
![]()


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥P–ABCD中,ABCD是矩形,PA=AB,E为PB的中点.
(1)若过C,D,E的平面交PA于点F,求证:F为PA的中点;
(2)若平面PAB⊥平面PBC,求证:BC⊥PA.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月22日,在韩国平昌冬奥会短道速滑男子![]() 米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子
米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子![]() 米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过
米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过![]() 个直道与弯道的交接口
个直道与弯道的交接口![]() .已知某男子速滑运动员顺利通过每个交接口的概率均为
.已知某男子速滑运动员顺利通过每个交接口的概率均为![]() ,摔倒的概率均为
,摔倒的概率均为![]() .假定运动员只有在摔倒或到达终点时才停止滑行,现在用
.假定运动员只有在摔倒或到达终点时才停止滑行,现在用![]() 表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.
表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.

(1)求该运动员停止滑行时恰好已顺利通过![]() 个交接口的概率;
个交接口的概率;
(2)求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知海岛![]() 在海岛
在海岛![]() 北偏东
北偏东![]() ,
,![]() ,
,![]() 相距
相距![]() 海里,物体甲从海岛
海里,物体甲从海岛![]() 以
以![]() 海里/小时的速度沿直线向海岛
海里/小时的速度沿直线向海岛![]() 移动,同时物体乙从海岛
移动,同时物体乙从海岛![]() 沿着海岛
沿着海岛![]() 北偏西
北偏西![]() 方向以
方向以![]() 海里/小时的速度移动.
海里/小时的速度移动.
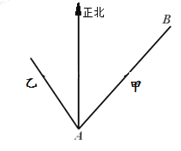
(1)问经过多长时间,物体甲在物体乙的正东方向;
(2)求甲从海岛![]() 到达海岛
到达海岛![]() 的过程中,甲、乙两物体的最短距离.
的过程中,甲、乙两物体的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
(I)求应从小学、中学、大学中分别抽取的学校数目。
(II)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com