
【题目】如图: ![]() 为
为![]() 所在平面外一点,
所在平面外一点, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() 于
于![]() .求证:
.求证:
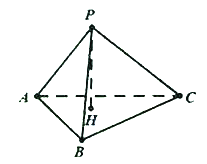
(1)![]() 是
是![]() 的垂心;
的垂心;
(2)![]() 为锐角三角形.
为锐角三角形.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1) 连接![]() 并延长交
并延长交![]() 与点
与点![]() 由三条侧棱
由三条侧棱![]() ,
, ![]() 两两垂直可以得到
两两垂直可以得到![]() 平面
平面![]() ,进而得到
,进而得到![]() ,由
,由![]() 平面
平面![]() ,可得
,可得![]() ,故∴
,故∴![]() 平面
平面![]() ,
,
,即可得![]() , 同理可证:
, 同理可证: ![]() ,
, ![]() ,可得
,可得![]() 是
是![]() 的垂心.
的垂心.
(2)可以通过余弦定理解决.
试题解析:证明:(1)连接![]() 并延长交
并延长交![]() 与点
与点![]() ,连接
,连接![]() .
.

∵![]() ,
, ![]() ,
, ![]()
∴img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/29/14/092b1670/SYS201712291412523815724471_DA/SYS201712291412523815724471_DA.027.png" width="39" height="17" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />平面![]()
∵直线![]() 在平面
在平面![]() 内
内
∴![]()
又∵![]() 平面
平面![]()
∴![]()
又![]()
∴![]() 平面
平面![]()
又∵直线![]() 在平面
在平面![]() 内
内
∴![]()
连接![]() 并延长交
并延长交![]() 与点
与点![]() ,连接
,连接![]() ;连接
;连接![]() 并延长交
并延长交![]() 与点
与点![]() ,连接
,连接![]() .
.
同理可证: ![]() ,
, ![]()
故![]() 是
是![]() 的垂心.
的垂心.
(2)设![]() ,
, ![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
, ![]() .
.
∵![]()
∴![]() 为锐角.
为锐角.
同理可证: ![]()
![]() 也为锐角
也为锐角
故证得![]() 为锐角三角形.
为锐角三角形.
点晴:本题考查是空间的直线与平面的垂直问题和三角形是锐角三角形的证明.第一问充分借助已知条件与判定定理,证明直线与平面垂直,得直线与直线垂直,从而得![]() 是
是![]() 的垂心.关于第二问中的三角形是锐角三角形问题,解答时可以通过设边,由
的垂心.关于第二问中的三角形是锐角三角形问题,解答时可以通过设边,由![]() ,
, ![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,然后用余弦定理解决.
,然后用余弦定理解决.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() ,求
,求![]() 零点的个数;
零点的个数;
(3)若![]() 为整数,且当
为整数,且当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
(参考数据![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() ,设函数
,设函数![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)已知![]() 分别为三角形
分别为三角形![]() 的内角对应的三边长,
的内角对应的三边长, ![]() 为锐角,
为锐角, ![]() ,
, ![]() ,且
,且![]() 恰是函数
恰是函数![]() 在
在![]() 上的最大值,求
上的最大值,求![]() 和三角形
和三角形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】画出下列函数的图像,并根据图像说出函数y=f(x)的单调区间,以及在各单调区间上函数y=f(x)是增函数还是减函数。
(1)y=x2-5x-6; (2)y=|4-x2|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校进行体验,现得到所有男生的身高数据,从中随机抽取50人进行统计(已知这50个身高介于155 ![]() 到195
到195![]() 之间),现将抽取结果按如下方式分成八组:第一组
之间),现将抽取结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,…,第八组
,…,第八组![]() ,并按此分组绘制如图所示的频率分布直方图,其中第六组
,并按此分组绘制如图所示的频率分布直方图,其中第六组![]() 和第七组
和第七组![]() 还没有绘制完成,已知第一组与第八组人数相同,第六组和第七组人数的比为5:2.
还没有绘制完成,已知第一组与第八组人数相同,第六组和第七组人数的比为5:2.
(1)补全频率分布直方图;
(2)根据频率分布直方图估计这50位男生身高的中位数;
(3)用分层抽样的方法在身高为![]() 内抽取一个容量为5的样本,从样本中任意抽取2位男生,求这两位男生身高都在
内抽取一个容量为5的样本,从样本中任意抽取2位男生,求这两位男生身高都在![]() 内的概率.
内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() :
: ![]() ,以平面直角坐标系
,以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() :
: ![]() .
.
(1)将曲线![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的![]() 、2倍后得到曲线
、2倍后得到曲线![]() ,求
,求![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司有一款保险产品的历史收益率(收益率![]() 利润
利润![]() 保费收入)的频率分布直方图如图所示:
保费收入)的频率分布直方图如图所示:
(1)试估计这款保险产品的收益率的平均值;
(2)设每份保单的保费在20元的基础上每增加![]() 元,对应的销量为
元,对应的销量为![]() (万份).从历史销售记录中抽样得到如下5组
(万份).从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:
| 25 | 30 | 38 | 45 | 52 |
销量为 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
由上表,知![]() 与
与![]() 有较强的线性相关关系,且据此计算出的回归方程为
有较强的线性相关关系,且据此计算出的回归方程为![]() .
.

(ⅰ)求参数![]() 的值;
的值;
(ⅱ)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入
的线性关系,用(1)中求出的收益率的平均值作为此产品的收益率,试问每份保单的保费定为多少元时此产品可获得最大利润,并求出最大利润.注:保险产品的保费收入![]() 每份保单的保费
每份保单的保费![]() 销量.
销量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com