
【题目】已知函数f(x)=cos2ωx﹣sin2ωx+2 ![]() cosωxsinωx,其中ω>0,若f(x)相邻两条对称轴间的距离不小于
cosωxsinωx,其中ω>0,若f(x)相邻两条对称轴间的距离不小于 ![]()
(1)求ω的取值范围及函数f(x)的单调递增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,a= ![]() ,b+c=3,当ω最大时,f(A)=1,求sinBsinC的值.
,b+c=3,当ω最大时,f(A)=1,求sinBsinC的值.
【答案】
(1)解:由题意得,f(x)=cos2ωx﹣sin2ωx+2 ![]() cosωxsinωx
cosωxsinωx
=cos2ωx+ ![]() sin2ωx=
sin2ωx= ![]() ;
;
由ω>0得,函数f(x) 的周期T= ![]() =
= ![]() ,
,
∵f(x)相邻两条对称轴间的距离不小于 ![]() ,
,
∴ ![]() ,则
,则 ![]() ,解得0<ω≤1,
,解得0<ω≤1,
∴ω的取值范围是(0,1].
由 ![]() 得,
得,
![]() ,
,
∴f(x)的单调递增区间为 ![]()
(2)解:由(1)可知ω的最大值为1,
∴f(x)= ![]() ,由f(A)=1得
,由f(A)=1得 ![]() ,
,
由0<A<π得 ![]() ,∴
,∴ ![]() ,解得A=
,解得A= ![]() ,
,
由余弦定理得cosA= ![]() =
= ![]() ,
,
把a= ![]() 代入化简得,b2+c2﹣bc=3,
代入化简得,b2+c2﹣bc=3,
又b+c=3联立解得bc=2,
由正弦定理知 ![]() =2R(R为△ABC的外接圆半径),
=2R(R为△ABC的外接圆半径),
又2R= ![]() =
= ![]() =2,∴sinB=
=2,∴sinB= ![]() ,sinC=
,sinC= ![]() ,
,
∴sinBsinC= ![]()
【解析】(1)利用二倍角的正弦公式、余弦公式,两角和的正弦公式化简解析式,由三角函数的周期公式表示出,f(x)的最小正周期,结合条件列出不等式求出ω的范围,由正弦函数的增区间求出f(x)的递增区间;(2)由(1)化简f(A)=1,由A的范围和特殊角的三角函数值求出A,由条件和余弦定理求出bc的值,由正弦定理和条件求出sinB、sinC,即可求出sinBsinC的值.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:
【题目】大学生小王自主创业,在乡下承包了一块耕地种植某种水果,每季投入2万元,根据以往的经验,每季收获的此种水果能全部售完,且水果的市场价格和这块地上的产量具有随机性,互不影响,具体情况如表:

(Ⅰ)设![]() 表示在这块地种植此水果一季的利润,求
表示在这块地种植此水果一季的利润,求![]() 的分布列及期望;
的分布列及期望;
(Ⅱ)在销售收入超过5万元的情况下,利润超过5万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,甲船在A处,乙船在A处的南偏东45°方向,距A有9n mile并以20n mile/h的速度沿南偏西15°方向航行,若甲船以28n mile/h的速度航行,应沿什么方向,用多少h能尽快追上乙船?
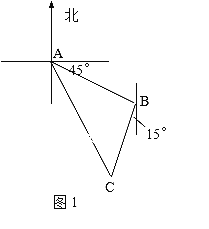
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.二进制数11010(2)化为八进制数为42(8)
B.若扇形圆心角为2弧度,且扇形弧所对的弦长为2,则这个扇形的面积为 ![]()
C.用秦九韶算法计算多项式f(x)=3x6+5x4+6x3﹣4x﹣5当x=3时的值时,v1=3v0+5=32
D.正切函数在定义域内为单调增函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择.
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率均为![]() ,第一次抽奖,若未中奖,则抽奖结束,若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖。规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,则获得1000元;若未中奖,则所获得奖金为0元.
,第一次抽奖,若未中奖,则抽奖结束,若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖。规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,则获得1000元;若未中奖,则所获得奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为![]() ,每次中奖均可获得奖金400元.
,每次中奖均可获得奖金400元.
(1)求某员工选择方案甲进行抽奖所奖金![]() (元)的分布列;
(元)的分布列;
(2)试比较某员工选择方案乙与选择方案甲进行抽奖,哪个方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD﹣A1B1C1D1的棱长为1,BD∩AC=0,M是线段D1O上的动点,过点M做平面ACD1的垂线交平面A1B1C1D1于点N,则点N到点A距离的最小值为( ) 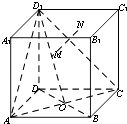
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料,生产1扯皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如表所示:
| A | B | C |
甲 | 4 | 8 | 3 |
乙 | 5 | 5 | 10 |
现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车品乙种肥料,产生的利润为3万元、分别用x,y表示计划生产甲、乙两种肥料的车皮数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲、乙两种肥料,求出此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四边形ABCD中,已知AB=9,BC=6, ![]() =2
=2 ![]() .
.
(1)若四边形ABCD是矩形,求 ![]()
![]() 的值;
的值;
(2)若四边形ABCD是平行四边形,且 ![]()
![]() =6,求
=6,求 ![]() 与
与 ![]() 夹角的余弦值.
夹角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com