已知实数a满足0<a<2,直线l1:ax-2y-2a+4=0和l2:2x+a2y-2a2-4=0与两坐标轴围成一个四边形.
(1)求证:无论实数a如何变化,直线l1、l2必过定点.
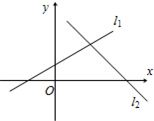
(2)画出直线l1和l2在平面坐标系上的大致位置.
(3)求实数a取何值时,所围成的四边形面积最小?
分析:(1)把所给的两个直线的方程进行整理,把含有字母a的部分都分开,提出a,得到一个直线的方程,把两个方程联立得到结果.
(2)根据所给的条件画出直线的大致位置,如图.
(3)求出直线与坐标轴的交点,把一个四边形转化成两个三角形,根据底边和高得到三角形的面积,表示出面积,根据二次函数的性质得到结果.
解答: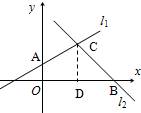
证明:(1)由l
1:ax-2y-2a+4=0变形得
a(x-2)-2y+4=0
所以,当x=2时,y=2
即直l
1过定点(2,2)
由l
2:2x+a
2y-2a
2-4=0变形得a
2(y-2)+2x-4=0
所以当y=2时,x=2
即直线l
2过定点(2,2)
(2)如图:
(3)直线l
1与y轴交点为A(0,2-a),直线l
2与x轴交点为B(a
2+2,0),如图
由直线l
1:ax-2y-2a+4=0知,直线l
1也过定点C(2,2)
过C点作x轴垂线,垂足为D,于是
S
四边形AOBC=S
梯形AODC+S
△BCD=
(2-a+2)•2+a2•2=a
2-a+4
∴当a=
时,S
四过形AOBC最小.
故当a=
时,所围成的四边形面积最小.
点评:本题考查过顶点的直线和四边形的面积的最值,本题解题的关键是表示出面积,在立体几何和解析几何中,不论求什么图形的面积一般都要表示出结果,再用函数的最值来求.


 证明:(1)由l1:ax-2y-2a+4=0变形得
证明:(1)由l1:ax-2y-2a+4=0变形得
