
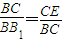 .∵
.∵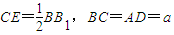 ,∴
,∴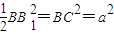 ,∴
,∴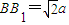 .…(5分)
.…(5分)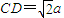 ,∴
,∴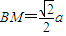 .
.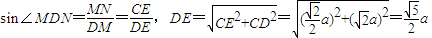 ,
,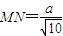 .在Rt△BMN中,
.在Rt△BMN中,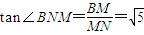 ,∴
,∴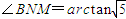 .
.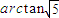 .…(9分)
.…(9分)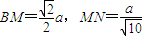 ,∴
,∴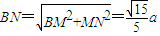 ,
,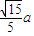 .…(12分)
.…(12分)

 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
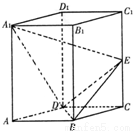
 如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A1D⊥BE.
如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A1D⊥BE.查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分12分)如图,已知直平行六面体ABCD—A![]() B
B![]() C
C![]() D
D![]() 中,AD⊥BD,AD=BD=a,E是CC
中,AD⊥BD,AD=BD=a,E是CC![]() 的中点,A1D⊥BE.
的中点,A1D⊥BE.
(1)求证:A![]() D⊥平面BDE;(2)求二面角B—DE—C的大小;(3)求点B到平面A
D⊥平面BDE;(2)求二面角B—DE—C的大小;(3)求点B到平面A![]() DE的距离.
DE的距离.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省高三上学期阶段验收数学试卷(解析版) 题型:解答题
(本题满分12分)
如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A1D⊥BE.

(I)求证:A1D⊥平面BDE;
(II)求二面角B―DE―C的大小;
(III)求点B到平面A1DE的距离
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com