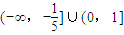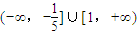【答案】
分析:根据f(1)=1,代入已知的等式中求出a的值,再把a的值代入等式得到一个关系式,记作①,把x换为
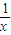
得到令一个关系式,记作②,把①代入②即可得到f(x)的解析式,把求出的f(x)代入不等式中,分x大于0和x小于0两种情况考虑,当x大于0时去分母时不等号方向不变,当x小于0时去分母不等号方向改变,分别求出相应的解集,求出两解集的并集即为原不等式的解集.
解答:解:因为f(1)=1,所以f(1)=af(1)-2,即a-2=1,解得a=3,
所以f(
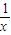
)=3f(x)-x-1①,
设
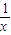
=t,得到f(t)=3f(

)-

-1,即f(x)=3f(
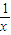
)-
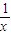
-1②,
将①代入②得:f(x)=3[3f(x)-x-1]-
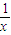
-1,
化简得:f(x)=
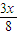
+
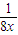
+

,
代入不等式得:
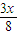
+
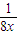
+

-x≥0,
当x>0时,去分母得:5x
2-4x-1≤0,即(5x+1)(x-1)≤0,
解得:-
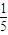
≤x≤1,所以原不等式的解集为(0,1];
当x<0时,去分母得:5x
2-4x-1≥0,即(5x+1)(x-1)≥0,
解得:x≥1或x≤-
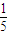
,所以原不等式的解集为(-∞,-
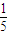
],
综上,原不等式的解集为(-∞,-
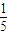
]∪(0,1].
故选A
点评:此题考查了其他不等式的解法,考查了分类讨论的数学思想,是一道中档题.确定出f(x)的解析式是解本题的关键.

 ,则不等式f(x)-x≥0的解集为( )
,则不等式f(x)-x≥0的解集为( )



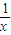 得到令一个关系式,记作②,把①代入②即可得到f(x)的解析式,把求出的f(x)代入不等式中,分x大于0和x小于0两种情况考虑,当x大于0时去分母时不等号方向不变,当x小于0时去分母不等号方向改变,分别求出相应的解集,求出两解集的并集即为原不等式的解集.
得到令一个关系式,记作②,把①代入②即可得到f(x)的解析式,把求出的f(x)代入不等式中,分x大于0和x小于0两种情况考虑,当x大于0时去分母时不等号方向不变,当x小于0时去分母不等号方向改变,分别求出相应的解集,求出两解集的并集即为原不等式的解集.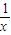 )=3f(x)-x-1①,
)=3f(x)-x-1①,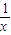 =t,得到f(t)=3f(
=t,得到f(t)=3f( )-
)- -1,即f(x)=3f(
-1,即f(x)=3f(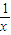 )-
)-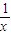 -1②,
-1②,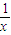 -1,
-1,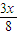 +
+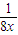 +
+ ,
,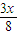 +
+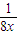 +
+ -x≥0,
-x≥0,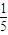 ≤x≤1,所以原不等式的解集为(0,1];
≤x≤1,所以原不等式的解集为(0,1];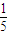 ,所以原不等式的解集为(-∞,-
,所以原不等式的解集为(-∞,-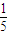 ],
],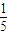 ]∪(0,1].
]∪(0,1].

 阅读快车系列答案
阅读快车系列答案 ,则不等式f(x)-x≥0的解集为( )
,则不等式f(x)-x≥0的解集为( )



 ,则不等式f(x)-x≥0的解集为( )
,则不等式f(x)-x≥0的解集为( )