
【题目】已知动点M到点N(1,0)和直线l:x=﹣1的距离相等. (Ⅰ)求动点M的轨迹E的方程;
(Ⅱ)已知不与l垂直的直线l'与曲线E有唯一公共点A,且与直线l的交点为P,以AP为直径作圆C.判断点N和圆C的位置关系,并证明你的结论.
【答案】解:(Ⅰ)设动点M(x,y),
由抛物线定义可知点M的轨迹E是以N(1,0)为焦点,直线l:x=﹣1为准线的抛物线,
所以轨迹E的方程为y2=4x.
(Ⅱ)点N在以PA为直径的圆C上.
理由:由题意可设直线l':x=my+n,
由 ![]() 可得y2﹣4my﹣4n=0(*),
可得y2﹣4my﹣4n=0(*),
因为直线l'与曲线E有唯一公共点A,
所以△=16m2+16n=0,即n=﹣m2.
所以(*)可化简为y2﹣4my+4m2=0,
所以A(m2,2m),
令x=﹣1得 ![]() ,
,
因为n=﹣m2,
所以 ![]()
所以NA⊥NP,
所以点N在以PA为直径的圆C上
【解析】(Ⅰ)利用抛物线的定义,即可求动点M的轨迹E的方程;(Ⅱ)由题意可设直线l':x=my+n,由 ![]() 可得y2﹣4my﹣4n=0,求出A,P的坐标,利用向量的数量积,即可得出结论.
可得y2﹣4my﹣4n=0,求出A,P的坐标,利用向量的数量积,即可得出结论.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某班开展一次智力竞赛活动,共a,b,c三个问题,其中题a满分是20分,题b,c满分都是25分.每道题或者得满分,或者得0分.活动结果显示,全班同学每人至少答对一道题,有1名同学答对全部三道题,有15名同学答对其中两道题.答对题a与题b的人数之和为29,答对题a与题c的人数之和为25,答对题b与题c的人数之和为20.则该班同学中只答对一道题的人数是;该班的平均成绩是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() ,g(x)=ax+b.
,g(x)=ax+b.
(1)若函数h(x)=f(x)﹣g(x)在(0,+∞)上单调递增,求实数a的取值范围;
(2)若直线g(x)=ax+b是函数f(x)=lnx﹣ ![]() 图象的切线,求a+b的最小值;
图象的切线,求a+b的最小值;
(3)当b=0时,若f(x)与g(x)的图象有两个交点A(x1 , y1),B(x2 , y2),求证:x1x2>2e2 .
(取e为2.8,取ln2为0.7,取 ![]() 为1.4)
为1.4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求证: ![]() ;
;
(3)判断曲线y=f(x)是否位于x轴下方,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中.点M不与点O重合,称射线OM与圆x2+y2=1的交点N为点M的“中心投影点“. ⑴点M(1, ![]() )的“中心投影点”为
)的“中心投影点”为
⑵曲线x2 ![]() 上所有点的“中心投影点”构成的曲线的长度是 .
上所有点的“中心投影点”构成的曲线的长度是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,他在《数学九章》中提出的多项式的秦九韶算法,至今仍是比较先进的算法,如图是事项该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为( ) 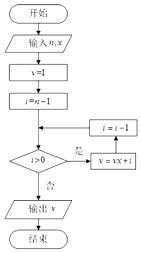
A.5
B.12
C.25
D.50
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥ABCD﹣A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C. 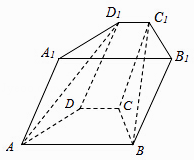
(1)求证:AD1⊥BC;
(2)若直线DD1与直线AB所成角为 ![]() ,求平面ABC1D1与平面ABCD所成角(锐角)的余弦值函数值.
,求平面ABC1D1与平面ABCD所成角(锐角)的余弦值函数值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax(lnx﹣1)(a≠0).
(1)求函数y=f(x)的单调递增区间;
(2)当a>0时,设函数g(x)= ![]() x3﹣f(x),函数h(x)=g′(x),
x3﹣f(x),函数h(x)=g′(x),
①若h(x)≥0恒成立,求实数a的取值范围;
②证明:ln(1×2×3×…×n)2e<12+22+32+…+n2(n∈N*).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com