
(14分)已知函数 ,其中a是实数.设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2.
,其中a是实数.设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2.
(Ⅰ)指出函数f(x)的单调区间;
(Ⅱ)若函数f(x)的图象在点A,B处的切线互相垂直,且x2<0,证明:x2﹣x1≥1;
(Ⅲ)若函数f(x)的图象在点A,B处的切线重合,求a的取值范围.
(Ⅰ)函数f(x)的单调减区间(﹣∞,﹣1),函数f(x)的单调增区间[﹣1,0),(0,+∞)
(Ⅱ)见解析
(Ⅲ)(﹣ln2﹣1,+∞)
【解析】(I)函数f(x)的单调减区间(﹣∞,﹣1),函数f(x)的单调增区间[﹣1,0),(0,+∞);
(II)由导数的几何意义知,点A处的切线的斜率为f′(x1),点B处的切线的斜率为f′(x2),
函数f(x)的图象在点A,B处的切线互相垂直时,有f′(x1)f′(x2)=﹣1,
当x<0时,(2x1+2)(2x2+2)=﹣1,∵x1<x2<0,∴2x1+2<0,2x2+2>0,
∴x2﹣x1=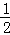 [﹣(2x1+2)+(2x2+2)]≥
[﹣(2x1+2)+(2x2+2)]≥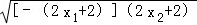 =1,
=1,
∴若函数f(x)的图象在点A,B处的切线互相垂直,有x2﹣x1≥1;
(III)当x1<x2<0,或0<x1<x2时,f′(x1)≠f′(x2),故x1<0<x2,
当x1<0时,函数f(x)在点A(x1,f(x1))处的切线方程为y﹣(x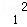 +2x1+a)=(2x1+2)(x﹣x1);
+2x1+a)=(2x1+2)(x﹣x1);
当x2>0时,函数f(x)在点B(x2,f(x2))处的切线方程为y﹣lnx2=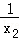 (x﹣x2);
(x﹣x2);
两直线重合的充要条件是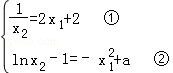 ,
,
由①及x1<0<x2得0<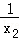 <2,由①②得a=lnx2+(
<2,由①②得a=lnx2+(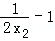 )2﹣1=﹣ln
)2﹣1=﹣ln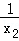 +
+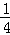 (
(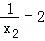 )2﹣1,
)2﹣1,
令t=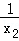 ,则0<t<2,且a=
,则0<t<2,且a=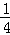 t2﹣t﹣lnt,设h(t)=
t2﹣t﹣lnt,设h(t)=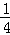 t2﹣t﹣lnt,(0<t<2)
t2﹣t﹣lnt,(0<t<2)
则h′(t)=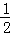 t﹣1﹣
t﹣1﹣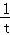 =
=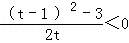 ,∴h(t)在(0,2)为减函数,
,∴h(t)在(0,2)为减函数,
则h(t)>h(2)=﹣ln2﹣1,∴a>﹣ln2﹣1,
∴若函数f(x)的图象在点A,B处的切线重合,a的取值范围(﹣ln2﹣1,+∞).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| π |
| 6 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市西城区高三二模理科数学试卷(解析版) 题型:选择题
已知函数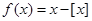 ,其中
,其中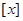 表示不超过实数
表示不超过实数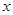 的最大整数.若关于
的最大整数.若关于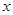 的方程
的方程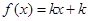 有三个不同的实根,则实数
有三个不同的实根,则实数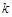 的取值范围是( )
的取值范围是( )
(A)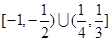 (B)
(B)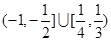
(C)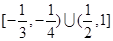 (D)
(D)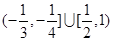
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| π |
| 6 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年江苏省南通中学高二(下)期末数学模拟试卷(理科)(解析版) 题型:填空题
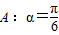 ,
,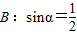 ;(2)A:x=1,B:x2+(a2-1)x-a2=0(a为实常数);(3)A:定义域为R上的函数f(x)满足f(1)>f(2),B:定义域为R的函数f(x)是单调减函数.其中A是B的充分不必要条件的是 .(填写所有满足要求的条件组的序号)
;(2)A:x=1,B:x2+(a2-1)x-a2=0(a为实常数);(3)A:定义域为R上的函数f(x)满足f(1)>f(2),B:定义域为R的函数f(x)是单调减函数.其中A是B的充分不必要条件的是 .(填写所有满足要求的条件组的序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com