
分析 根据题意,问题转化为a≥-x-$\frac{1}{x}$;即求x∈(0,$\frac{3}{2}}$]时-(x+$\frac{1}{x}$)的最大值即可.
解答 解:不等式x2+ax+1≥0对一切x∈(0,$\frac{3}{2}}$]成立,
∴ax≥-x2-1,
即a≥-x-$\frac{1}{x}$=-(x+$\frac{1}{x}$);
由x∈(0,$\frac{3}{2}}$],
∴x+$\frac{1}{x}$≥2$\sqrt{x•\frac{1}{x}}$=2,当且仅当x=1时“=”成立,
即-(x+$\frac{1}{x}$)的最大值是-2;
∴a的最小值是-2.
故答案为:-2.
点评 本题考查了转化法与转化思想的应用问题,也考查了一元二次不等式的应用问题,是中档题.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 年龄(岁) | 35岁及以下 | (35,50) | 50岁以上 |
| 人数(人) | 220 | 180 | 100 |
| A. | 22 | B. | 18 | C. | 10 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在某次测量中得到的A样本的茎叶图如图所示,则该样本的中位数、众数、极差分别是( )
在某次测量中得到的A样本的茎叶图如图所示,则该样本的中位数、众数、极差分别是( )| A. | 47,45,56 | B. | 46,45,53 | C. | 45,47,53 | D. | 46,45,56 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
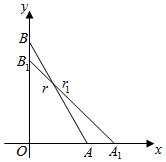 如图,长为4的线段AB的两个端点A和B分别在x轴正半轴和y正半轴上滑动,T为AB的中点,∠OAB=75°,当线段AB滑动到A1B1位置时,∠OA1B1=45°.线段在滑动时点T运动到T1点,则点T运动的路程为$\frac{π}{3}$.
如图,长为4的线段AB的两个端点A和B分别在x轴正半轴和y正半轴上滑动,T为AB的中点,∠OAB=75°,当线段AB滑动到A1B1位置时,∠OA1B1=45°.线段在滑动时点T运动到T1点,则点T运动的路程为$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小值-6 | B. | 最大值-6 | C. | 最小值-2 | D. | 最小值-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com