
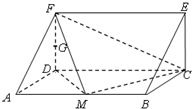
 如图,在三棱柱ADF-BCE中,侧棱AB⊥底面ADF,底面ADF是等腰直角三角形,且AD=DF=a,AB=2a,M、G分别是AB、DF的中点.
如图,在三棱柱ADF-BCE中,侧棱AB⊥底面ADF,底面ADF是等腰直角三角形,且AD=DF=a,AB=2a,M、G分别是AB、DF的中点.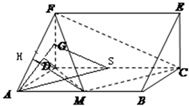 解:(1)证明:取DC中点S,连接AS、GS、GA,
解:(1)证明:取DC中点S,连接AS、GS、GA,
| ||
| 2 |
| 2 |
| DH |
| DM |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
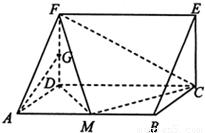
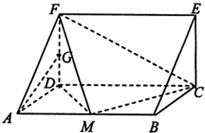 (2013•贵阳二模)如图,在三棱柱ADF-BCE中,侧棱AB底面ADF,底面ADF是等腰直角三角形,且AD=DF=a,AB=2a,G是线段DF的中点,M是线段AB上一点.
(2013•贵阳二模)如图,在三棱柱ADF-BCE中,侧棱AB底面ADF,底面ADF是等腰直角三角形,且AD=DF=a,AB=2a,G是线段DF的中点,M是线段AB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:
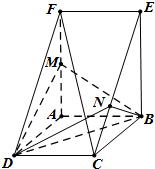 如图,在三棱柱ADF-BCE中,矩形ABCD和矩形ABEF所在的平面互相垂直,AF=2AB=2AD=2,M为AF的中点,BN⊥CE.
如图,在三棱柱ADF-BCE中,矩形ABCD和矩形ABEF所在的平面互相垂直,AF=2AB=2AD=2,M为AF的中点,BN⊥CE.查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省长沙市长望浏宁四县高三3月调研考试数学文卷 题型:解答题
(本小题满分12分)
如图,在三棱柱ADF—BCE中,侧棱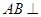 底面
底面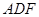 ,底面
,底面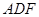 是等腰直角三角形,且
是等腰直角三角形,且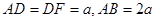 ,M、G分别是AB、DF的中点.
,M、G分别是AB、DF的中点.
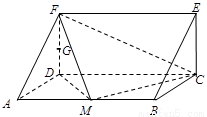
(1)求证GA∥平面FMC;
(2)求直线DM与平面ABEF所成角。
查看答案和解析>>
科目:高中数学 来源:2013年贵州省贵阳市高考数学二模试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com