
科目:高中数学 来源: 题型:
| ON |
| ON |
| 5 |
| OM |
| OT |
| M1M |
| N1N |
| OP |
| OA |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ON |
| ON |
| 5 |
| OM |
| OT |
| MM1 |
| NN1 |
| OP |
| OA |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省石家庄市高三第二次模拟理科数学试卷(解析版) 题型:解答题
在平面直角坐标系中,已知直线l:y=-1,定点F(0,1),过平面内动点P作PQ丄l于Q点,且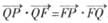 •
•
(I )求动点P的轨迹E的方程;
(II)过点P作圆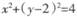 的两条切线,分别交x轴于点B、C,当点P的纵坐标y0>4时,试用y0表示线段BC的长,并求ΔPBC面积的最小值.
的两条切线,分别交x轴于点B、C,当点P的纵坐标y0>4时,试用y0表示线段BC的长,并求ΔPBC面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
设平面直角坐标中,O为原点,N为动点,![]() 过点M作
过点M作![]() 轴于M1,过N作
轴于M1,过N作![]() 丄x轴于点N1,
丄x轴于点N1,![]() ,记点R的轨迹为曲线C。
,记点R的轨迹为曲线C。
(I)求曲线C的方程;
(II )已知直线L与双曲线C1:![]() 的右支相交于P、Q两点(其中点P在第一象限),线段OP交轨迹C于A,若
的右支相交于P、Q两点(其中点P在第一象限),线段OP交轨迹C于A,若![]() ,
,![]() ,求直线L的方程
,求直线L的方程
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com