Question

3．已知|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2，且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°，求$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$的夹角，$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$的夹角．

Answer 1

分析 由题意画出图形，数形结合可得答案．

解答 解：由题意作图，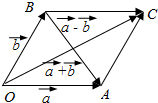

∵|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2，且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°，
∴四边形OACB为菱形，且∠BOA=60°，
则$\overrightarrow{OC}=\overrightarrow{a}+\overrightarrow{b}$，$\overrightarrow{BA}=\overrightarrow{a}-\overrightarrow{b}$，
∴$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$的夹角为30°，$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$的夹角为60°．

点评 本题考查平面向量的数量积运算，考查了向量的加减法法则，是中档题．