
【题目】如图,![]() 、
、![]() 是过点
是过点![]() 夹角为
夹角为![]() 的两条直线,且与圆心为
的两条直线,且与圆心为![]() ,半径长为
,半径长为![]() 的圆分别相切,设圆周上一点
的圆分别相切,设圆周上一点![]() 到
到![]() 、
、![]() 的距离分别为
的距离分别为![]() 、
、![]() ,那么
,那么![]() 的最小值为(____).
的最小值为(____).

【答案】![]()
【解析】
根据题意,分析可得|OM|=2,建立坐标系,分析可得l1、l2的关于y轴对称,据此设出直线l1与l2的方程,P(cosθ,sinθ),由此表示2d1+d2,结合三角函数的性质分析可得答案.
根据题意,l1、l2是过点M夹角为![]() 的两条直线,且与圆心为O,半径r=1的圆分别相切,
的两条直线,且与圆心为O,半径r=1的圆分别相切,
则|OM|=2r=2,
如图建立坐标系,以圆心O为坐标原点,OM为y轴建立坐标系,M(0,2),
又由l1、l2是过点M夹角为![]() 的两条直线,则l1、l2的关于y轴对称,
的两条直线,则l1、l2的关于y轴对称,
易得l1、l2的倾斜角为![]() 和
和![]() ,则设l1的方程为y
,则设l1的方程为y![]() x+2,l2的方程为y
x+2,l2的方程为y![]() x+2,
x+2,
P是圆周上的一个动点,设P(cosθ,sinθ),
则d1![]() 1
1![]() ,
,
d2![]() 1
1![]() ,
,
则2d1+d2=2+(![]() cosθ﹣sinθ)+1
cosθ﹣sinθ)+1![]() (
(![]() cosθ+sinθ)=3
cosθ+sinθ)=3![]() 3
3![]() sin(
sin(![]() θ)≥3
θ)≥3![]() ;
;
即2d1+d2的最小值为3![]() ;
;
故答案为:3![]() .
.


科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为D,若存在闭区间
的定义域为D,若存在闭区间![]() ,使得函数
,使得函数![]() 满足以下两个条件:(1)
满足以下两个条件:(1)![]() 在[m,n]上是单调函数;(2)
在[m,n]上是单调函数;(2)![]() 在[m,n]上的值域为[2m,2n],则称区间[m,n]为
在[m,n]上的值域为[2m,2n],则称区间[m,n]为![]() 的“倍值区间”.下列函数中存在“倍值区间”的有( )个.
的“倍值区间”.下列函数中存在“倍值区间”的有( )个.
①![]() ②
②![]() ③
③![]()
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (e为自然对数的底数,e=2.71828……),函数
(e为自然对数的底数,e=2.71828……),函数![]() 图象关于直线
图象关于直线![]() 对称,函数
对称,函数![]() 的最小值为m.
的最小值为m.
(I)求曲线![]() 的切线方程;
的切线方程;
(Ⅱ)求证:![]() ;
;
(III)求函数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.非零向量![]() 满足
满足![]() ,则
,则![]() 与
与![]() 的夹角为
的夹角为![]()
B.若![]() ,则
,则![]() 的夹角为锐角
的夹角为锐角
C.若![]() ,则
,则![]() 一定是直角三角形
一定是直角三角形
D.![]() 的外接圆的圆心为O,半径为1,若
的外接圆的圆心为O,半径为1,若![]() ,且
,且![]() ,则向量
,则向量![]() 在向量
在向量![]() 方向上的投影的数量为
方向上的投影的数量为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,已知点A(1,0)和点B(﹣1,0),![]() ,且∠AOC=x,其中O为坐标原点.
,且∠AOC=x,其中O为坐标原点.

(1)若x=![]() ,设点D为线段OA上的动点,求
,设点D为线段OA上的动点,求![]() 的最小值;
的最小值;
(2)若![]() R,求
R,求![]() 的最大值及对应的x值.
的最大值及对应的x值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,AC=BC=PC=2,AB=PA=PB=2![]() .
.
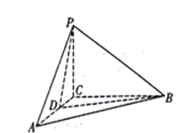
(1)证明:PC⊥平面ABC;
(2)若点D在棱AC上,且二面角D-PB-C为30°,求PD与平面PAB所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A、B、C所对的边分别是a、b、c,且有bcosC+ccosB=2acosB.
(1)求B的大小;
(2)若△ABC的面积是![]() ,且a+c=5,求b.
,且a+c=5,求b.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com