
【题目】函数![]() 的部分图像如图所示,将
的部分图像如图所示,将![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
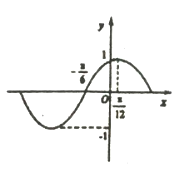
(1)求函数![]() 的解折式;
的解折式;
(2)在![]() 中,角
中,角![]() 满足
满足![]() ,且其外接圆的半径
,且其外接圆的半径![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
【答案】(1)sin![]() (2)
(2)![]()
【解析】
(1)由图知![]() =4
=4![]() ,解得ω=2.
,解得ω=2.
∵f![]() =sin
=sin![]() =1,∴
=1,∴![]() +φ=2kπ+
+φ=2kπ+![]() (k∈Z),即φ=2kπ+
(k∈Z),即φ=2kπ+![]() (k∈Z).
(k∈Z).
由-![]() <φ<
<φ<![]() ,得φ=
,得φ=![]() ,
,
∴f(x)=sin![]() ,
,
∴f![]() =sin
=sin![]() =sin
=sin![]() ,
,
即函数y=g(x)的解析式为g(x)=sin![]() .
.
(2)∵2sin2![]() =g
=g![]() +1,
+1,
∴1-cos(A+B)=1+sin![]() ,
,
∵cos(A+B)=-cosC,sin![]() =cos 2C,
=cos 2C,
于是上式变为cosC=cos 2C,即cosC=2cos2C-1,整理得2cos2C-cosC-1=0,
解得cosC=-![]() 或1(舍),∴C=
或1(舍),∴C=![]() π.
π.
由正弦定理得![]() =2R=4,解得c=2
=2R=4,解得c=2![]() ,
,
于是由余弦定理得cosC=-![]() =
=![]() ,∴a2+b2=12-ab≥2ab,∴ab≤4(当且仅当a=b时等号成立),
,∴a2+b2=12-ab≥2ab,∴ab≤4(当且仅当a=b时等号成立),
∴S△ABC=![]() absinC=
absinC=![]() ab≤
ab≤![]() .
.
∴△ABC的面积的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某企业对设备进行技术升级改造,为了检验改造效果,现从设备改造后生产的大量产品中抽取了100件产品作为样本,检测一项质量指标值,统计整理为如图所示的频率分布直方图:
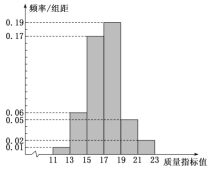
(1)估计该企业所生产产品的质量指标的平均数和中位数(中位数保留一位小数);
(2)若产品的质量指标在![]() 内,则该产品为残次品,生产并销售一件残次品该企业损失1万元;若产品的质量指标在
内,则该产品为残次品,生产并销售一件残次品该企业损失1万元;若产品的质量指标在![]() 范围内,则该产品为特优品,生产一件特优品该企业获利3万元.把样本中的残次品和特优品取出合并在一起,在从中任取2件产品进行销售,那么该企业收入为多少万元的可能性最大?
范围内,则该产品为特优品,生产一件特优品该企业获利3万元.把样本中的残次品和特优品取出合并在一起,在从中任取2件产品进行销售,那么该企业收入为多少万元的可能性最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的左、右焦点为F1,F2,设点F1,F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.
的左、右焦点为F1,F2,设点F1,F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.
(1)求椭圆C的标准方程;
(2)设A,B,P为椭圆C上三点,满足![]() ,记线段AB中点Q的轨迹为E,若直线l:y=x+1与轨迹E交于M,N两点,求|MN|.
,记线段AB中点Q的轨迹为E,若直线l:y=x+1与轨迹E交于M,N两点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=4sin(2x+![]() )(x∈R),有下列命题:
)(x∈R),有下列命题:
①y=f(x)的表达式可改写为y=4cos(2x﹣![]() );
);
②y=f(x)是以2π为最小正周期的周期函数;
③y=f(x)的图象关于点![]() 对称;
对称;
④y=f(x)的图象关于直线x=﹣![]() 对称.
对称.
其中正确的命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体P﹣ABCD中,平面ABCD⊥平面PAB ,四边形ABCD为矩形,△PAB为正三角形,若AB=2,AD=1,E,F 分别为AC,BP中点.

(1)求证:EF∥平面PCD;
(2)求直线DP与平面ABCD所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com