
【题目】已知函数f(x)是定义域为R上的奇函数,当x>0时,f(x)=x2+2x.
(1)求f(x)的解析式;
(2)若不等式f(t﹣2)+f(2t+1)>0成立,求实数t的取值范围.
【答案】
解:(1)∵函数f(x)是定义域为R上的奇函数,
∴f(x)=﹣f(﹣x)
又∵当x>0时,f(x)=x2+2x.
若x>0,则﹣x<0.f(﹣x)=(﹣x)2+2(﹣x)=x2﹣2x
∴f(x)=﹣f(﹣x)=2x﹣x2 .
∴f(x)=![]() ;
;
(2)当x>0时,f(x)=x2+2x=(x+1)2﹣1,
区间(0,+∞)在对称轴x=﹣1的右边,为增区间,
由奇函数的性质,可得f(x)在R上递增.
不等式f(t﹣2)+f(2t+1)>0即为
f(1+2t)>﹣f(t﹣2)=f(2﹣t),
即有1+2t>2﹣t,解得t>![]()
则t的取值范围是(![]() ,+∞).
,+∞).
【解析】(1)运用奇函数的定义,可得x<0的解析式,进而得到f(x)的解析式;
(2)求出f(x)在R上递增.不等式f(t﹣2)+f(2t+1)>0即为f(1+2t)>﹣f(t﹣2)=f(2﹣t),即有1+2t>2﹣t,解不等式即可得到所求范围.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米,某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-![]() 表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)当k=2时,求炮的射程;
(2)求炮的最大射程;
(3)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以其中它?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车的出现方便了人们的出行,深受市民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)频率分布直方图.
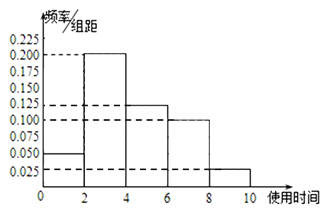
(1)已知该校大一学生有2400人,求抽取的100名学生中大一学生人数;
(2)根据频率分布直方图求该校大学生每周使用共享单车的平均时间.
(3)![]() 从抽取的100个样本中,用分层抽样的方法抽取使用共享单车时间超过6小时同学5人,再从这5人中任选2人,求这2人使用共享单车时间都不超过8小时的概率.
从抽取的100个样本中,用分层抽样的方法抽取使用共享单车时间超过6小时同学5人,再从这5人中任选2人,求这2人使用共享单车时间都不超过8小时的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=AA1=![]() , ∠ABC=60°.
, ∠ABC=60°.
(1)证明:AB⊥A1C;
(2)求二面角A﹣A1C﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个“乱点鸳鸯谱”节目:每次邀请四对青年夫妻,先由每人随机抽签获得顺序展示才艺,再由观众通过投票的方式实施男女配对(观众不知道他们的真实配对情况).
(Ⅰ)求正确配对家庭数的期望;
(Ⅱ)设有![]() 对夫妻,记他们完全错位的配对种类总数为
对夫妻,记他们完全错位的配对种类总数为![]() .
.
①求![]() ,
, ![]() ,
, ![]() ;
;
②推导![]() ,
, ![]() ,
, ![]() 所满足的关系式.
所满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com