
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() ,
,![]() 的中点.
的中点.
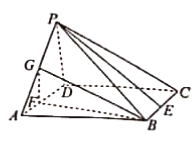
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
科目:高中数学 来源: 题型:
【题目】今年1月至2月由新型冠状病毒引起的肺炎病例陡然增多,为了严控疫情传播,做好重点人群的预防工作,某地区共统计返乡人员![]() 人,其中
人,其中![]() 岁及以上的共有
岁及以上的共有![]() 人.这
人.这![]() 人中确诊的有
人中确诊的有![]() 名,其中
名,其中![]() 岁以下的人占
岁以下的人占![]() .
.
(1)请将下面的列联表补充完整,并判断是否有![]() %的把握认为是否确诊患新冠肺炎与年龄有关;
%的把握认为是否确诊患新冠肺炎与年龄有关;
确诊患新冠肺炎 | 未确诊患新冠肺炎 | 合计 | |
50岁及以上 | 40 | ||
50岁以下 | |||
合计 | 10 | 100 |
(2)为了研究新型冠状病毒的传染源和传播方式,从![]() 名确诊人员中随机抽出
名确诊人员中随机抽出![]() 人继续进行血清的研究,
人继续进行血清的研究,![]() 表示被抽取的
表示被抽取的![]() 人中
人中![]() 岁以下的人数,求
岁以下的人数,求![]() 的分布列以及数学期望.
的分布列以及数学期望.
参考表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式: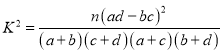 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的两个顶点
的两个顶点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,且
,且![]() 所在直线的斜率之积等于
所在直线的斜率之积等于![]() ,记顶点
,记顶点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求顶点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 在曲线
在曲线![]() 上,且
上,且![]() 为
为![]() 的重心(
的重心(![]() 为坐标原点),求证:
为坐标原点),求证:![]() 的面积为定值,并求出该定值.
的面积为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一对夫妇为了给他们的独生孩子支付将来上大学的费用,从孩子一周岁生日开始,每年到银行储蓄![]() 元一年定期,若年利率为
元一年定期,若年利率为![]() 保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为
保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代十进制的算筹计数法,在数学史上是一个伟大的创造,算筹实际上是一根根同长短的小木棍.如图,是利用算筹表示数![]() 的一种方法.例如:3可表示为“
的一种方法.例如:3可表示为“![]() ”,26可表示为“
”,26可表示为“![]() ”.现有6根算筹,据此表示方法,若算筹不能剩余,则可以用
”.现有6根算筹,据此表示方法,若算筹不能剩余,则可以用![]() 这9数字表示两位数的个数为
这9数字表示两位数的个数为![]()
![]()
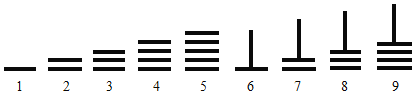
A.13B.14C.15D.16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com