
(本小题满分l2分)(注意:在试题卷上作答无效)
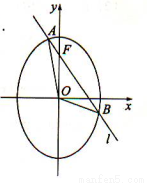
已知 为坐标原点,
为坐标原点,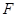 为椭圆
为椭圆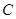 :
: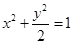 在
在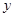 轴正半轴上的焦点,过
轴正半轴上的焦点,过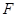 且斜率为
且斜率为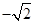 的直线
的直线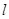 与
与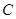 交与
交与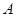 、
、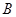 两点,点
两点,点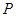 满足
满足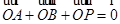 .
.
(I)证明:点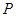 在
在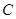 上;
上;
(II)设点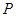 关于点
关于点 的对称点为
的对称点为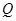 ,证明:
,证明: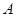 、
、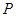 、
、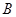 、
、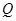 四点在同一圆上.
四点在同一圆上.
(I)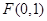 ,
,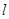 的方程为
的方程为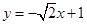 ,代入
,代入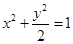 并化简得
并化简得
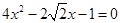 .
…………………………2分
.
…………………………2分
设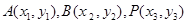 ,
,
则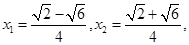
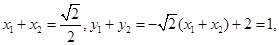
由题意得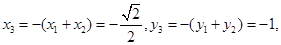
所以点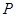 的坐标为
的坐标为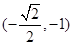 .
.
经验证点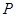 的坐标
的坐标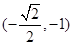 满足方程
满足方程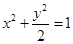 ,故点
,故点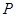 在椭圆
在椭圆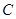 上
…6分
上
…6分
(II)由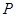
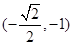 和题设知,
和题设知,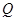
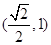 ,
,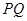 的垂直平分线
的垂直平分线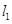 的方程为
的方程为
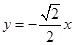 .
①
.
①
设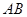 的中点为
的中点为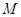 ,则
,则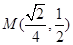 ,
,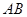 的垂直平分线
的垂直平分线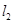 的方程为
的方程为
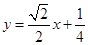 .
②
.
②
由①、②得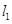 、
、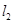 的交点为
的交点为 . …………………………9分
. …………………………9分
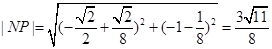 ,
,
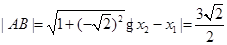 ,
,
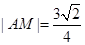 ,
,
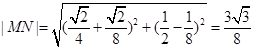 ,
,
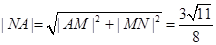 ,
,
故
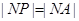 ,
,
又
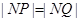 ,
,
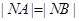 ,
,
所以
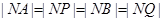 ,
,
由此知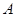 、
、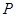 、
、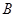 、
、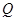 四点在以
四点在以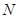 为圆心,
为圆心,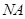 为半径的圆上. ……………12分
为半径的圆上. ……………12分
(II)法二: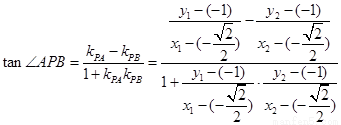
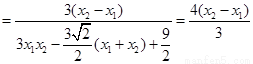
同理
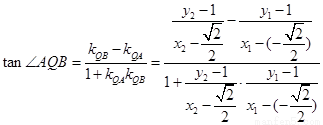
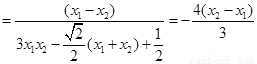
所以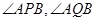 互补,
互补,
因此A、P、B、Q四点在同一圆上。
【解析】本题涉及到平面向量,有一定的综合性和计算量,完成有难度. 首先出题位置和平时模拟几乎没有变化,都保持全卷倒数第二道题的位置,这点考生非常适应的。相对来讲比较容易,是因为这道题最好特点没有任何的未知参数,我们看这道题椭圆完全给出,直线过了椭圆焦点,并且斜率也给出,平时做题斜率不给出,需要通过一定条件求出来,或者根本求不出来,这道题都给了,反而同学不知道怎么下手,让我求什么不知道,给出马上给向量条件,出了两道证明题,这个跟平时做的不太一样,证明题结论给大家,需要大家严谨推导出来,可能叙述的时候有不严谨的地方。这两问出的非常巧妙,非常涉及解析几何本质的内容,一个证明点在椭圆上的问题,还有一个疑问既然出现四点共圆,这都是平时很少涉及内容。从侧面体现教育深层次的问题,让学生掌握解析几何的本质,而不是把套路解决。其实几年前上海考到解析几何本质问题,最后方法用代数方法研究几何的问题,什么是四点共圆?首先在同一个圆上,首先找到圆心,四个点找圆形不好找,最简单的两个点怎么找?这是平时的知识,怎么找距离相等的点,一定在中垂线,两个中垂线交点必然是圆心,找到圆心再距离四个点距离相等,这就是简单的计算问题.方法确定以后计算量其实比往年少.


科目:高中数学 来源:2011-2012学年山东省高三下学期模拟冲刺考试理科数学试卷(解析版) 题型:解答题
(本小题满分l2分)已知数列{an}中,a1=1,a2=3且2an+1=an+2+an(n∈N*).数列{bn}的前n项和为Sn,其中b1=- ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*).
(1)求数列{an}和{bn}的通项公式;
(2)若Tn= +
+ +…+
+…+ ,求Tn的表达式
,求Tn的表达式
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三下学期模拟冲刺考试理科数学试卷(解析版) 题型:解答题
(本小题满分l2分)已知椭圆的的右顶点为A,离心率 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)证明以线段 为直径的圆经过焦点
为直径的圆经过焦点 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年贵州省高三年级第五次月考文科数学 题型:解答题
(本小题满分l2分)(注意:在试题卷上作答无效)
求经过A(2,-1),和直线x+y=1相切,且圆心在直线y=-2x上的圆的方程
(I)求出圆的标准方程
(II)求出(I)中的圆与直线3x+4y=0相交的弦长AB
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省高三上学期10月月考理科数学卷 题型:解答题
(本小题满分l2分)设命题 :函数
:函数 (
( )的值域是
)的值域是 ;命题
;命题 :指数函数
:指数函数 在
在 上是减函数.若命题“
上是减函数.若命题“ 或
或 ”是假命题,求实数
”是假命题,求实数 的范围.
的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com