
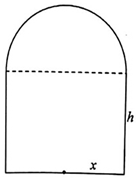
 某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.
某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.分析 (1)根据体积公式求出h,再根据表面积公式计算即可得到S与x的关系式,
(2)根据导数和函数的最值得关系即可求出.
解答 解:(1)据题意,可知πx2h=3π,得$h=\frac{3}{x^2}$,
$S=\frac{1}{2}•4π{x^2}+π{x^2}+2πx•\frac{3}{x^2}=3π{x^2}+\frac{6π}{x},(x>0)$
(2)${S^'}=6πx-\frac{6π}{x^2}$,
令S′=0,得x=±1,舍负,
当S′(x)>0时,解得x>1,函数S(x)单调递增,
当S′(x)<0时,解得0<x<1,函数S(x)单调递减,
故当x=1时,函数有极小值,且是最小值,S(1)=9π
答:当圆柱的底面半径为1时,可使表面积S取得最小值9π.
点评 本题考查了导数与函数的最值在实际生活中的应用,属于中档题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -$\frac{1}{2}$ | C. | 1或-$\frac{1}{2}$ | D. | -1或-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com