Question

1．已知在三棱锥A-BCD中，AB=CD，且点M，N分别是BC，AD的中点．
（1）若直线AB与CD所成的角为60°，则直线AB和MN所成的角为60°．
（2）若直线AB⊥CD，则直线AB与MN所成的角为45．

Answer 1

分析 （1）取AC中点E，连结NE、ME，则ME$\underset{∥}{=}$$\frac{1}{2}AB$，NE$\underset{∥}{=}$$\frac{1}{2}CD$，∠EMN是直线AB和MN所成的角，由直线AB与CD所成的角为60°，得∠MEN=60°，由此能求出直线AB和MN所成的角．
（2）取AC中点E，连结NE、ME，则ME$\underset{∥}{=}$$\frac{1}{2}AB$，NE$\underset{∥}{=}$$\frac{1}{2}CD$，∠EMN是直线AB和MN所成的角，由AB⊥CD°，得∠MEN=90°，由此能求出直线AB和MN所成的角．

解答 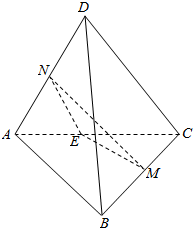解：（1）取AC中点E，连结NE、ME，如图，
∵三棱锥A-BCD中，AB=CD，且点M，N分别是BC，AD的中点，
∴ME$\underset{∥}{=}$$\frac{1}{2}AB$，NE$\underset{∥}{=}$$\frac{1}{2}CD$，∴NE=ME，
∠EMN是直线AB和MN所成的角，
∵直线AB与CD所成的角为60°，∴∠MEN=60°，
∴∠EMN=60°．
故答案为：60°．
（2）取AC中点E，连结NE、ME，如图，
∵三棱锥A-BCD中，AB=CD，且点M，N分别是BC，AD的中点，
∴ME$\underset{∥}{=}$$\frac{1}{2}AB$，NE$\underset{∥}{=}$$\frac{1}{2}CD$，∴NE=ME，
∠EMN是直线AB和MN所成的角，
∵AB⊥CD，∴∠MEN=90°，
∴∠EMN=45°．
故答案为：45°．

点评 本题考查异面直线所成角的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．