
【题目】已知函数f(x)=|ax-2|,不等式f(x)≤4的解集为{x|-2≤x≤6}.
(1)求实数a的值;
(2)设g(x)=f(x)+f(x+3),若存在x∈R,使g(x)-tx≤2成立,求实数t的取值范围.
【答案】(1)1;(2)![]() .
.
【解析】
(1)利用绝对值不等式的解法求得-2≤![]()
![]() ≤6,对
≤6,对![]() 的正负分类讨论,结合不等式
的正负分类讨论,结合不等式![]() 的解集为
的解集为![]() 列方程,即可得解
列方程,即可得解
(2)由(1)可得![]() ,将
,将![]() 转化成
转化成![]() ,分别作出
,分别作出![]() 及
及![]() 的简图,“存在
的简图,“存在![]() ,使
,使![]() 成立”,转化成
成立”,转化成![]() 的图象与直线y=tx+2相交,由图列不等式即可得解。
的图象与直线y=tx+2相交,由图列不等式即可得解。
(1)由|![]()
![]() -2|≤4得-4≤
-2|≤4得-4≤![]()
![]() -2≤4,即-2≤
-2≤4,即-2≤![]()
![]() ≤6,
≤6,
当![]() >0时,
>0时,![]() ,所以
,所以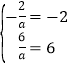 ,解得
,解得![]() =1;
=1;
当![]() <0时,
<0时,![]() ,所以
,所以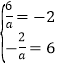 ,无解.
,无解.
所以实数![]() 的值为1.
的值为1.
(2)由已知g(x)=f(x)+f(x+3)=|x+1|+|x-2|=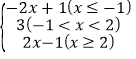 ,
,
不等式g(x)-tx≤2转化成g(x)≤tx+2,
由题意知![]() 的图象与直线y=tx+2相交,作出对应图象
的图象与直线y=tx+2相交,作出对应图象
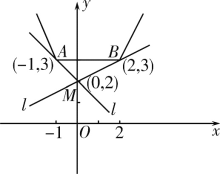
由图得,当t<0时,t≤kAM;当t>0时,t≥kBM,
又因为kAM=-1,![]() ,
,
所以t≤-1或![]() ,
,
即t∈(-∞,-1]∪[![]() ,+∞).
,+∞).


科目:高中数学 来源: 题型:
【题目】某校举办《国学》知识问答中,有一道题目有5个选项A,B,C,D,E,并告知考生正确选项个数不超过3个,满分5分,若该题正确答案为![]() ,赋分标准为“选对1个得2分,选对2个得4分,选对3个得5分,每选错1个扣3分,最低得分为0分”.假定考生作答的答案中的选项个数不超过3个.
,赋分标准为“选对1个得2分,选对2个得4分,选对3个得5分,每选错1个扣3分,最低得分为0分”.假定考生作答的答案中的选项个数不超过3个.
(1)若张小雷同学无法判断所有选项,只能猜,他在犹豫答案是“任选1个选项作为答案”或者“任选2个选项作为答案”或者“任选3个选项作为答案”,以得分期望为决策依据,则他的最佳方案是哪一种?说明理由.
(2)已知有10名同学的答案都是3个选项,且他们的答案互不相同,他们此题的平均得分为x分.现从这10名同学中任选3名,计算得到这3名考生此题得分的平均分为y分,试求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x-1,![]() (a∈R),若对任意x1∈[1,+∞),总存在x2∈R,使f(x1)=g(x2),则实数a的取值范围是( )
(a∈R),若对任意x1∈[1,+∞),总存在x2∈R,使f(x1)=g(x2),则实数a的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() (α为参数),在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,点M的极坐标为
(α为参数),在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,点M的极坐标为![]() ,直线l的极坐标方程为
,直线l的极坐标方程为![]() .
.
(1)求直线l的直角坐标方程与曲线C的普通方程;
(2)若N是曲线C上的动点,P为线段MN的中点,求点P到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,对于点
中,对于点![]() ,定义变换
,定义变换![]() :将点
:将点![]() 变换为点
变换为点![]() ,使得
,使得![]() 其中
其中![]() .这样变换
.这样变换![]() 就将坐标系
就将坐标系![]() 内的曲线变换为坐标系
内的曲线变换为坐标系![]() 内的曲线.则四个函数
内的曲线.则四个函数![]() ,
,![]() ,
,![]() ,
,![]() 在坐标系
在坐标系![]() 内的图象,变换为坐标系
内的图象,变换为坐标系![]() 内的四条曲线(如图)依次是
内的四条曲线(如图)依次是
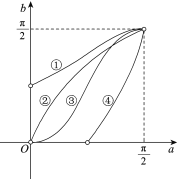
A. ②,③,①,④B. ③,②,④,①C. ②,③,④,①D. ③,②,①,④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查生活规律与患胃病是否与有关,某同学在当地随机调查了200名30岁以上的人,并根据调查结果制成了不完整的列联表如下:
不患胃病 | 患胃病 | 总计 | |
生活有规律 | 60 | 40 | |
生活无规律 | 60 | 100 | |
总计 | 100 |
(1)补全列联表中的数据;
(2)用独性检验的基本原理,说明生活无规律与患胃病有关时,出错的概率不会超过多少?
参考公式和数表如下:
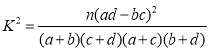
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com