
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的方程为
的方程为![]() ,若直线
,若直线![]() 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆![]() 有公共点,则
有公共点,则![]() 的最大值为__________.
的最大值为__________.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】动圆M与定圆C:x2+y2+4x=0相外切,且与直线l:x-2=0相切,则动圆M的圆心的轨迹方程为( )
A. y2-12x+12=0 B. y2+12x-12=0
C. y2+8x=0 D. y2-8x=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业投资公司拟投资开发某种新能源产品,估计能获得10万元到1000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)若建立函数y=f(x)模型制定奖励方案,试用数学语言表述该公司对奖励函数f(x)模型的基本要求,并分析函数y= ![]() 是否符合公司要求的奖励函数模型,并说明原因;
是否符合公司要求的奖励函数模型,并说明原因;
(2)若该公司采用模型函数y= ![]() 作为奖励函数模型,试确定最小的正整数a的值.
作为奖励函数模型,试确定最小的正整数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A={x|x2-ax+a2-19=0},B={ x|x2-5x+6=0},C={x|x2+2x-8=0},且![]()
![]() (A∩B),A∩C=
(A∩B),A∩C=![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的右焦点为F(1,0),且点(﹣1,
的右焦点为F(1,0),且点(﹣1, ![]() )在椭圆C上.
)在椭圆C上.
(1)求椭圆C的标准方程;
(2)已知动直线l过点F,且与椭圆C交于A,B两点,试问x轴上是否存在定点Q,使得 ![]() 恒成立?若存在,求出点Q的坐标,若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱![]() 中,底面
中,底面![]() 是边长为2的正三角形,
是边长为2的正三角形, ![]() 是棱
是棱![]() 的中点,且
的中点,且![]() .
.
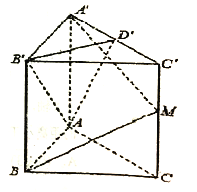
(1)若点![]() 为棱
为棱![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)若点![]() 在棱
在棱![]() 上,且
上,且![]() 平面
平面![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点与抛物线
的右焦点与抛物线![]() 的焦点重合,且该椭圆的离心率与双曲线
的焦点重合,且该椭圆的离心率与双曲线![]() 的离心率互为倒数.
的离心率互为倒数.
(1)求椭圆的方程;
(2)设直线![]() 与椭圆相交于不同的两点
与椭圆相交于不同的两点![]() ,已知点
,已知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在线段
在线段![]() 的垂直平分线上,且
的垂直平分线上,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,D是AC的中点,A1D⊥平面ABC,AB=BC,平面BB1D与棱A1C1交于点E.
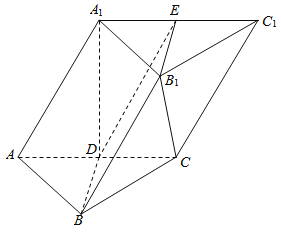
(1)求证:AC⊥A1B;
(2)求证:平面BB1D⊥平面AA1C1C;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com