
【题目】已知四棱锥P-ABCD的体积为![]() ,其三视图如图所示,其中正视图为等腰三角形,侧视图为直角三角形,俯视图是直角梯形.
,其三视图如图所示,其中正视图为等腰三角形,侧视图为直角三角形,俯视图是直角梯形.

(1)求正视图的面积;
(2)求四棱锥P-ABCD的侧面积.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据四棱锥的体积得PA=![]() ,进而得正视图的面积;
,进而得正视图的面积;
(2)过A作AE∥CD交BC于E,连接PE,确定四个侧面积面积S△PAB,S△PAD, S△PCD, S△PBC求和即可.
试题解析:
(1) 如图所示四棱锥P-ABCD的高为PA,底面积为S=![]() ·CD=
·CD=![]() ×1=
×1=![]()
∴四棱锥P-ABCD的体积V四棱锥P-ABCD=![]() S·PA=
S·PA=![]() ×
×![]() ·PA=
·PA=![]() ,∴PA=
,∴PA=![]()
∴正视图的面积为S=![]() ×2×
×2×![]() =
=![]() .
.
(2)如图所示,过A作AE∥CD交BC于E,连接PE.根据三视图可知,E是BC的中点,
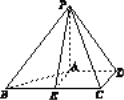
且BE=CE=1,AE=CD=1,且BC⊥AE,AB=![]()
又PA⊥平面ABCD,∴PA⊥BC,PA⊥DC,PD=![]() ,∴BC⊥面PAE,∴BC⊥PE,
,∴BC⊥面PAE,∴BC⊥PE,
又DC⊥AD,∴DC⊥面PAD,∴DC⊥PD,且PA⊥平面ABCD.∴PA⊥AE,
∴PE2=PA2+AE2=3.∴PE=![]() .
.
∴四棱锥P-ABCD的侧面积为
S=S△PAB+ S△PAD+ S△PCD+ S△PBC=![]() ·
·![]() ·
·![]() +
+![]() ·
·![]() ·1+
·1+![]() ·1·
·1·![]() +
+![]() ·2·
·2·![]() =
=![]() .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图象过点
的图象过点![]() ,且与
,且与![]() 轴有唯一的交点
轴有唯一的交点![]() .
.
(1)求![]() 的表达式;
的表达式;
(2)设函数![]() ,若
,若![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,记此函数的最小值为
,记此函数的最小值为![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga ![]() (a>0且a≠1)是奇函数.
(a>0且a≠1)是奇函数.
(1)求实数m的值;
(2)判断函数f(x)在区间(1,+∞)上的单调性并说明理由;
(3)当x∈(n,a﹣2)时,函数f(x)的值域为(1,+∞),求实数n,a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)已知f( ![]() +1)=x+2
+1)=x+2 ![]() ,求f(x)的解析式;
,求f(x)的解析式;
(2)已知f(x)是一次函数,且满足3f(x+1)﹣2f(x﹣1)=2x+17,求f(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,侧棱
,侧棱![]() ,底面
,底面![]() 为直角梯形,其中
为直角梯形,其中![]() 为
为![]() 中点.
中点.
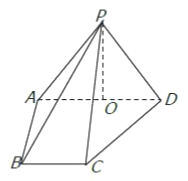
(1)求证: ![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)线段![]() 上是否存在
上是否存在![]() ,使得它到平面
,使得它到平面![]() 的距离为
的距离为![]() ?若存在,求出
?若存在,求出![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市在发展过程中,交通状况逐渐受到有关部门的关注,据有关统计数据显示,从上午6点到中午12点,车辆通过该市某一路段的用时y(分钟)与车辆进入该路段的时刻t之间的关系可近似地用如下函数给出: y= 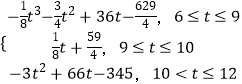
求从上午6点到中午12点,通过该路段用时最多的时刻.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体P﹣ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC= ![]() .
. 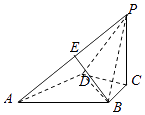
(1)求证:PA⊥BD;
(2)已知E是PA上一点,且BE∥平面PCD.若PC=2,求点E到平面ABCD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com