
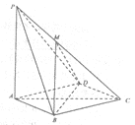
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() .底面
.底面![]() 是菱形,
是菱形,![]() .
.
(Ⅰ)求证:直线![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正切值;
所成角的正切值;
(Ⅲ)已知![]() 在线段
在线段![]() 上,且
上,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(I)见解析;(II)![]() ;(III)
;(III)![]()
【解析】
(I)由菱形的性质,得AC⊥BD;由PA⊥平面ABCD证出PA⊥BD,结合AC、PA是平面PAC内的相交直线,可得BD⊥平面PAC;
(II)过B作BE⊥AD于点E,连结PE.由PA⊥平面ABCD得PA⊥BE,结合PA∩AD=A证出BE⊥平面PAD,可得∠BPE就是直线PB与平面PAD所成角.Rt△BPE中,利用三角函数的定义算出tan∠BPE![]() ,即得结果;
,即得结果;
(III)设F为CM的中点,连结BF、DF,由等腰△BMC与等腰△DMC有公共的底面,证出∠BFD为二面角B﹣MC﹣D的平面角.然后在△BFD中,利用余弦定理,算出cos∠BFD,即得结果.
(I)∵底面ABCD是菱形,∴AC⊥BD
∵PA⊥平面ABCD,BD平面ABCD,∴PA⊥BD
又∵AC、PA是平面PAC内的相交直线,
∴直线BD⊥平面PAC;
(II)过B作BE⊥AD于点E,连结PE
∵PA⊥平面ABCD,BE平面ABCD,∴PA⊥BE
∵BE⊥AD,PA∩AD=A
∴BE⊥平面PAD,可得∠BPE就是直线PB与平面PAD所成角
∵Rt△BPE中,BE![]() ,PE
,PE![]()
∴tan∠BPE![]() ,即PB与平面PAD所成角的正切值等于
,即PB与平面PAD所成角的正切值等于![]() ;
;
(III)设F为CM的中点,连结BF、DF
∵△BMC中,BM=BC,∴BF⊥CM.同理可得DF⊥CM
∴∠BFD就是二面角B﹣MC﹣D的平面角
在△BFD中,BD=2,BF=DF![]() ,
,
∴由余弦定理,得cos∠BFD![]()
由此可得二面角B﹣MC﹣D的余弦值等于![]() .
.


科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图一)的平面展开图(如图二)中,四边形
(如图一)的平面展开图(如图二)中,四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若点![]() 在棱
在棱![]() 上运动,当直线
上运动,当直线![]() 与平面
与平面![]() 所成的角最大时,求二面角
所成的角最大时,求二面角![]() 的余弦值.
的余弦值.
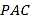
图一
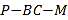
图二
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为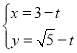 (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程
的方程![]() ,
,
(1)求直线![]() 和圆
和圆![]() 的直角坐标方程;
的直角坐标方程;
(3)设圆![]() 与直线
与直线![]() 交于点
交于点![]() 、
、![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点为
,左、右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且点
上,且点![]() 关于原点对称,直线
关于原点对称,直线![]() 的斜率的乘积为
的斜率的乘积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 经过点
经过点![]() ,且与椭圆
,且与椭圆![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() ,判断直线
,判断直线![]() 的斜率是否为定值?若是,请求出该定值;若不是,请说明理由.
的斜率是否为定值?若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产零件的流水线上随机抽取100个零件作为样本,测量其直径后,整理得到如表:
生产零件的流水线上随机抽取100个零件作为样本,测量其直径后,整理得到如表:
直径/ | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行评判(
,并根据以下不等式进行评判(![]() 表示相应事件的频率):①
表示相应事件的频率):①![]() ;②
;②![]() ;③
;③![]() .评判规则为:若同时满足上述三个不等式,则设备性能等级为甲;仅满足其中两个,则设备性能等级为乙;若仅满足其中一个,则设备性能等级为丙;若全部不满足,则设备性能等级为丁.试判断设备
.评判规则为:若同时满足上述三个不等式,则设备性能等级为甲;仅满足其中两个,则设备性能等级为乙;若仅满足其中一个,则设备性能等级为丙;若全部不满足,则设备性能等级为丁.试判断设备![]() 的性能等级.
的性能等级.
(2)将直径小于等于![]() 或直径大于
或直径大于![]() 的零件认为是次品.
的零件认为是次品.
(i)从设备![]() 的生产流水线上任意抽取2个零件,计算其中次品个数
的生产流水线上任意抽取2个零件,计算其中次品个数![]() 的数学期望
的数学期望![]() ;
;
(ii)从样本中任意抽取2个零件,计算其中次品个数![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的各棱长均为2,侧面
的各棱长均为2,侧面![]()
![]() 底面
底面![]() ,侧棱
,侧棱![]() 与底面
与底面![]() 所成的角为
所成的角为![]() .
.
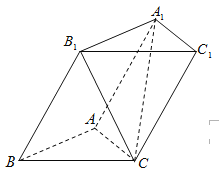
(Ⅰ)求直线![]() 与底面
与底面![]() 所成的角;
所成的角;
(Ⅱ)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(5分)《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第五节的容积为( )
A. 1升 B. ![]() 升 C.
升 C. ![]() 升 D.
升 D. ![]() 升
升
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com