
解析:设A(x1,y1)、B(x2,y2),代入抛物线方程并作差得k AB=![]() =
=![]() ,
,
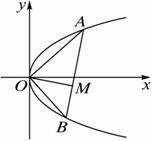
∴直线AB的方程l AB:y-y1=![]() (x-x1).?
(x-x1).?
注意到y12=4x1,y1y2=-16(∵k OA·k OB=-1,?
∴![]() ·
·![]() =-1
=-1![]()
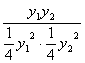 =-1
=-1![]() y1y2=-16),
y1y2=-16),
即得(y1+y2)y+16=4x.
又直线OM的方程为y=-![]() x,?
x,?
由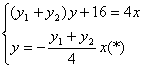
![]() x2+y2-4x=0(x≠0)即为所求的轨迹方程.
x2+y2-4x=0(x≠0)即为所求的轨迹方程.
温馨提示:由(*)消去y1+y2所得方程为所求,是因为由(*)解出x、y(用y1+y2作已知)得到的是点M的坐标,而点M的坐标的关系式(即消去y1+y2得x、y的关系)为动点M的轨迹方程.显然这样做与直接过渡其关系式是一样的.另外本题还可以设OA的斜率为k,类似于上面的方法求M的轨迹方程.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com