练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某地区规划道路建设，考虑道路铺设方案，方案设计图中，求表示城市，两点之间连线表示两城市间可铺设道路，连线上数据表示两城市间铺设道路的费用，要求从任一城市都能到达其余各城市，并且铺设道路的总费用最小．例如：在三个城市道路设计中，若城市间可铺设道路的线路图如图1，则最优设计方案如图2，此时铺设道路的最小总费用为10．现给出该地区可铺设道路的线路图如图3，则铺设道路的最小总费用为（　　）
    分析：确定铺设道路的总费用最小时的线路，即可求得铺设道路的最小总费用．
    解答：解：由题意，铺设道路的总费用最小时的线路为：A→E→F→G→D，从G分叉，G→C→B
    总费用为2+3+1+2+3+5=16
    故答案为：16
    点评：本题考查统筹方法在实际中的应用，考查学生阅读能力，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    某地区规划道路建设，需考虑道路铺设方案．方案设计图中，点表示城市，两点之间连线表示两城市间可铺设道路，连线上数据表示两城市间铺设道路的费用，要求从任一城市都能到达其余各城市，并且铺设道路的总费用最小．例如：在三个城市道路设计中，若城市间可铺设道路的线路图如图1，则最优设计方案如图2，此时铺设道路的最小总费用为l0．现给出该地区可铺设道路的线路图如图3，则铺设道路的最小总费用为
    16
    16
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

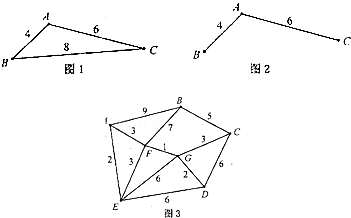
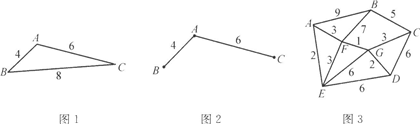
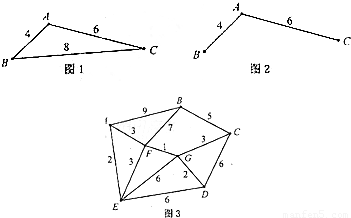
    某地区规划道路建设，考虑道路铺设方案．方案设计图中，点表示城市，两点之间连线表示两城市间可铺设道路，边线上数据表示两城市间铺设道路的费用，要求从任一城市都能到达其余各城市，并且铺设道路的总费用最小．例如：在三个城市道路设计中，若城市间可铺设道路的线路图如图1，则最优设计方案如图2，此时铺设道路的最小总费用为10.

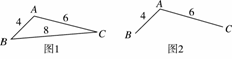
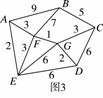
    现给出该地区可铺设道路的线路图如图3，则铺设道路的最小费用为________．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山东省青岛二中高三（上）9月月考数学试卷（文科）（解析版） 题型：选择题

    某地区规划道路建设，考虑道路铺设方案，方案设计图中，求表示城市，两点之间连线表示两城市间可铺设道路，连线上数据表示两城市间铺设道路的费用，要求从任一城市都能到达其余各城市，并且铺设道路的总费用最小．例如：在三个城市道路设计中，若城市间可铺设道路的线路图如图1，则最优设计方案如图2，此时铺设道路的最小总费用为10．现给出该地区可铺设道路的线路图如图3，则铺设道路的最小总费用为（ ）

    A．11
    B．9
    C．16
    D．18

    查看答案和解析>>

    科目：高中数学 来源：2012年全国普通高等学校招生统一考试文科数学（福建卷解析版） 题型：填空题

    某地区规划道路建设，考虑道路铺设方案，方案设计图中，求表示城市，两点之间连线表示两城市间可铺设道路，连线上数据表示两城市间铺设道路的费用，要求从任一城市都能到达其余各城市，并且铺设道路的总费用最小。例如：在三个城市道路设计中，若城市间可铺设道路的线路图如图1，则最优设计方案如图2，此时铺设道路的最小总费用为10.

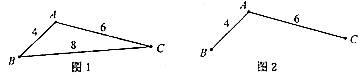
    现给出该地区可铺设道路的线路图如图3，则铺设道路的最小总费用为____________。

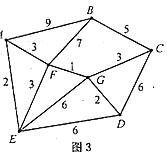
    【解析】走线路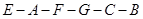最消费用16.

     

    查看答案和解析>>

    同步练习册答案