
分析 本题必须保证:①使loga(3-ax)有意义,即a>0且a≠1,3-ax>0.②使loga(3-ax)在[0,2]上是x的减函数.由于所给函数可分解为y=logau,u=3-ax,其中u=2-ax在a>0时为减函数,所以必须a>1;③[0,1]必须是y=loga(3-ax)定义域的子集.
解答 解:因为f(x)在[0,2]上是x的减函数,所以根据复合函数的单调性得出:$\left\{\begin{array}{l}{a>1}\\{3-2a>0}\end{array}\right.$
即1$<a<\frac{3}{2}$
故答案为:1<a<$\frac{3}{2}$
点评 本题综合了多个知识点,需要概念清楚,推理正确.(1)复合函数的单调性;(2)真数大于零


科目:高中数学 来源: 题型:选择题
| A. | [5a,-2a) | B. | (-∞,5a]∪(-2a,+∞) | C. | (-2a,5a]? | D. | (-∞,5a] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
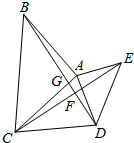 如图,△ABC中,AB=AC,∠BAC=90°,∠ABD=∠ACE,CE=BD,
如图,△ABC中,AB=AC,∠BAC=90°,∠ABD=∠ACE,CE=BD,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com